题目内容
11．有一拦水坝横断面是一个等腰梯形，它的上底为6m，下底长为10m，高为2m，则此拦水坝的坡度与坡角分别为（ ）| A． | 1：1，45° | B． | $\sqrt{3}$：1，30° | C． | $\sqrt{3}$：1，45° | D． | $\sqrt{3}$：1，60° |
分析 作AE⊥BC于点E，在直角△ABE中求得BE的长，在直角△ABC中根据边角关系即可求解．
解答 
解：作AE⊥BC于点E．
则BE=$\frac{1}{2}$（BC-AD）=$\frac{1}{2}$（10-6）=2（cm）．
则△ABE是等腰直角三角形．
故坡角是45°，坡度是1：1．
故选A．
点评 本题考查了坡度、坡角的定义，正确作出辅助线转化为直角三角形的计算是关键．
练习册系列答案
相关题目
2．
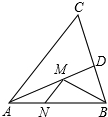如图，在锐角△ABC中，AB=8，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（ ）
如图，在锐角△ABC中，AB=8，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（ ）| A． | 8 | B． | 6 | C． | $4\sqrt{2}$ | D． | $3\sqrt{2}$ |
将下列数填入如图所示的相应集合（圈）内．
6．方程（m+2）x|m|+3mx+4=0是关于x的一元二次方程，则（ ）
| A． | m≠±2 | B． | m=±2 | C． | m=2 | D． | m=-2 |
20．下列各式计算正确的是（ ）
| A． | $\frac{a+c}{a+b}=\frac{c}{b}$ | B． | $\frac{a-c}{-a+b}=-\frac{a-c}{a+b}$ | ||
| C． | $\frac{x^8}{x^2}={x^4}$ | D． | $\frac{b}{{3{a^2}}}+\frac{1}{6ab}=\frac{{2{b^2}+a}}{{6{a^2}b}}$ |