题目内容
2.设a=$\sqrt{8-x}$,b=2,c=$\sqrt{6}$.(1)当a有意义时,求x的取值范围.
(2)若a、b、c为Rt△ABC三边长,求x的值.
分析 (1)利用二次根式的性质得出x的取值范围;
(2)分别利用①当a2+b2=c2,②当a2+c2=b2,③当b2+c2=a2,求出即可.
解答 解:(1)∵a有意义,
∴8-x≥0,
∴x≤8;
(2)方法一:分三种情况:
①当a2+b2=c2,即8-x+4=6,得x=6,
②当a2+c2=b2,即8-x+6=4,得x=10,
③当b2+c2=a2,即4+6=8-x,得x=-2,
又∵x≤8,
∴x=6或-2;
方法二:∵直角三角形中斜边为最长的边,c>b
∴存在两种情况,
①当a2+b2=c2,即8-x+4=6,得x=6,
②当b2+c2=a2,即4+6=8-x,得x=-2,
∴x=6或-2.
点评 此题主要考查了二次根式的应用以及勾股定理等知识,利用分类讨论得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
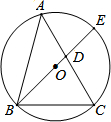 定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.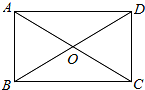 如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,则对角线AC的长度为8.
如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,则对角线AC的长度为8.