题目内容
17.一次函数y=2x+1的图象与x轴的交点坐标为(-$\frac{1}{2}$,0).分析 令y=0可求得x的值,则可求得与x轴的交点坐标.
解答 解:在y=2x+1中令y=0,可得2x+1=0,解得x=-$\frac{1}{2}$,
∴一次函数y=2x+1的图象与x轴的交点坐标为(-$\frac{1}{2}$,0),
故答案为:(-$\frac{1}{2}$,0).
点评 本题主要考查一次函数与坐标轴的交点,掌握函数图象与坐标轴的交点所满足的条件是解题的关键.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
8.已知抛物线y=ax2-2ax-a+1的顶点在x轴上,则a的值是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 1 |
6.下列式子成立的是( )
| A. | $\frac{1}{\sqrt{3}}$=$\sqrt{3}$ | B. | 2$\sqrt{3}$-$\sqrt{3}$=2 | C. | $\sqrt{(-3)^{2}}$=3 | D. | ($\sqrt{3}$)2=6 |
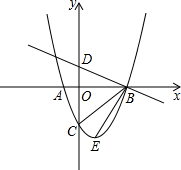 如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.
如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.