题目内容
11.若直线y1上的每个点都可以表示为($\frac{1}{2}$m-2,m),且直线y1和y轴交点为点A,和直线y2=x交点为点B,若点O为坐标原点,则△AOB的面积为8.分析 根据直线y1上的每个点都可以表示为($\frac{1}{2}$m-2,m),且直线y1和y轴交点为点A,得到方程$\frac{1}{2}$m-2=0,求得m=4,得到A(0,4),由于直线y1和直线y2=x交点为点B,得到方程m-2=m,求得m=-4,得到B(-4,-4),于是结论可得.
解答 解:∵直线y1上的每个点都可以表示为($\frac{1}{2}$m-2,m),且直线y1和y轴交点为点A,
∴$\frac{1}{2}$m-2=0,
解得:m=4,
∴A(0,4),
∵直线y1和直线y2=x交点为点B,
∴$\frac{1}{2}$m-2=m,
∴m=-4,
∴B(-4,-4),
∴S△AOB=$\frac{1}{2}$×4×4=8,
故答案为:8.
点评 本题考查了两直线相交或平行的问题,一次函数图形上点的坐标特征,正确理解题意是解题的关键.

练习册系列答案
相关题目
1.计算(a3)3÷(-a2)4的结果是( )
| A. | a4 | B. | a3 | C. | a2 | D. | a |
19.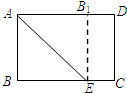 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 6cm |
6.下列式子成立的是( )
| A. | $\frac{1}{\sqrt{3}}$=$\sqrt{3}$ | B. | 2$\sqrt{3}$-$\sqrt{3}$=2 | C. | $\sqrt{(-3)^{2}}$=3 | D. | ($\sqrt{3}$)2=6 |
16.下列实数中,无理数是( )
| A. | -$\frac{5}{3}$ | B. | $\sqrt{7}$ | C. | |-2| | D. | $\root{3}{8}$ |