题目内容
14.已知$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$是方程2x-ay=9的一个解,解决下列问题:(1)求a的值;
(2)化简并求值:(a-1)(a+1)-2(a-1)2+a(a-3).
分析 (1)把x、y的值代入方程可求得a的值;
(2)根据乘法公式先化简,再把a的值代入求值即可.
解答 解:(1)∵$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$是方程2x-ay=9的一个解,
∴6-a=9,解得a=-3;
(2)(a-1)(a+1)-2(a-1)2+a(a-3)
=a2-1-2(a2-2a+1)+a2-3a
=a2-1-2a2+4a-2+a2-3a
=a-3,
把a=-3代入上式可得:原式=-3-3=-6.
点评 本题主要考查方程解的概念,掌握方程的解满足方程是解题的关键.

练习册系列答案
相关题目
19.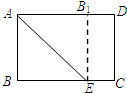 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 6cm |
6.下列式子成立的是( )
| A. | $\frac{1}{\sqrt{3}}$=$\sqrt{3}$ | B. | 2$\sqrt{3}$-$\sqrt{3}$=2 | C. | $\sqrt{(-3)^{2}}$=3 | D. | ($\sqrt{3}$)2=6 |
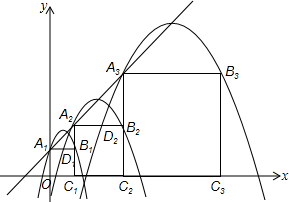 在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).