题目内容
12. 定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.(1)已知某一勾股三角形的三个内角度数从小到大依次为x°、y°和z°,且xy=2160,求x+y的值;
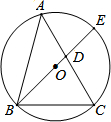
(2)如图,△ABC是⊙O的内接三角形,AB=$\sqrt{6}$,AC=$1+\sqrt{3}$,BC=2,BE是⊙O的直径,交AC于D.
①求证:△ABC是勾股三角形;②求DE的长.
分析 (1)根据内角和定理,题中新定义,以及已知等式求出x+y的值即可;
(2)①过B作BH垂直于AC,设AH=x,表示出CH,利用勾股定理表示出BH,再利用勾股定理列出关于x的方程,求出方程的解得到x的值,表示出AH,BH,HC,利用题中新定义判断即可得证;
②连接CE,利用圆周角定理得到三角形BCE为等腰直角三角形,根据BC与CE的长求出BE的长,过D作DK垂直于AB,设KD=h,表示出BK与AK的长,根据AK+BK=AB关于h的方程,求出方程的解得到h的值,即可求出DE的长.
解答 解:(1)由题意可得:$\left\{\begin{array}{l}{xy=2160①}\\{{x}^{2}+{y}^{2}={z}^{2}②}\\{x+y+z=180③}\end{array}\right.$,
由③得:z=180-(x+y),
代入②得:(x+y)2-2xy=[180°-(x+y)]2,
把①代入得:x+y=102;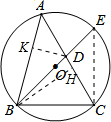 (2)①过B作BH⊥AC于H,设AH=x,则CH=1+$\sqrt{3}$-x,
(2)①过B作BH⊥AC于H,设AH=x,则CH=1+$\sqrt{3}$-x,
Rt△ABH中,BH=$\sqrt{6-{x}^{2}}$,
Rt△CBH中,根据勾股定理得:6-x2+(1+$\sqrt{3}$-x)2=4,
解得:x=$\sqrt{3}$,
∴AH=BH=$\sqrt{3}$,HC=1,
∴∠A=45°,∠ABC=75°,∠C=60°,
∵452+602=752,
∴△ABC是勾股三角形;
②连接CE,则∠BEC=∠BAC=45°,
又∵BE是直径,
∴∠BCE=90°,
∴BC=CE=2,BE=2$\sqrt{2}$,
过D作DK⊥AB于K,设KD=h,则BK=$\sqrt{3}$h,AK=h,
由AB=AK+BK=($\sqrt{3}$+1)h=$\sqrt{6}$,得到h=$\frac{3\sqrt{2}-\sqrt{6}}{2}$,
∴BD=3$\sqrt{2}$-$\sqrt{6}$,
则DE=BE-BD=$\sqrt{6}$-$\sqrt{2}$.
点评 此题属于圆综合题,涉及的知识有:勾股定理,内角和定理,圆周角定理,弄清题中的新定义是解本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | a4 | B. | a3 | C. | a2 | D. | a |
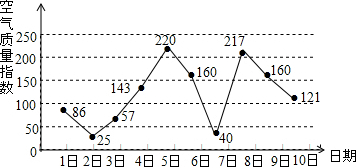 如图,气象局预报某市6月10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染的概率是$\frac{3}{4}$.
如图,气象局预报某市6月10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染的概率是$\frac{3}{4}$.
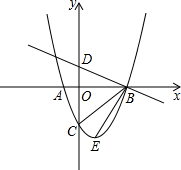 如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.
如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.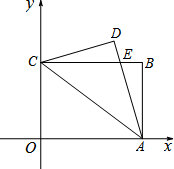 已知:如图,平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(4,0),(0,3).将△OCA沿直线CA翻折,得到△DCA,且DA交CB于点E.
已知:如图,平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(4,0),(0,3).将△OCA沿直线CA翻折,得到△DCA,且DA交CB于点E.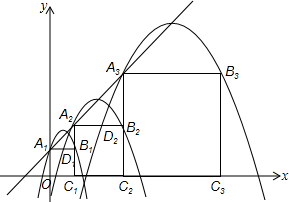 在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).