题目内容
16.计算:(1)$\sqrt{2}$×$\sqrt{5}$
(2)$\sqrt{3}$×$\sqrt{12}$
(3)2$\sqrt{6}$×$\sqrt{\frac{1}{2}}$
(4)$\sqrt{288}$×$\sqrt{\frac{1}{72}}$.
分析 根据二次根式的乘法,即可解答.
解答 解:(1)$\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$;
(2)$\sqrt{3}$×$\sqrt{12}$=$\sqrt{36}$=6;
(3)2$\sqrt{6}$×$\sqrt{\frac{1}{2}}$=2$\sqrt{3}$;
(4)$\sqrt{288}$×$\sqrt{\frac{1}{72}}$=$\sqrt{4}$=2.
点评 本题考查了二次根式的乘法,解决本题的关键是熟记二次根式的乘法法则.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
8.在下列各组二次根式中,不是可以合并的二次根式的一组是( )
| A. | $\sqrt{3ab^2}$和$\sqrt{3ab^2c}$ | B. | $\sqrt{12ab^3}$和$\sqrt{3ab}$ | C. | $\sqrt{ab}$和$\sqrt{{a}^{3}{b}^{5}}$ | D. | $\sqrt{\frac{b}{a}}$和$\sqrt{\frac{a}{b}}$ |
5.利用二次函数y=x2-2x-2的图象求一元二次方程y=x2-2x-2的近似解时,画图如图1示并进一步估算其中一根列表如下,根据这些信息,可得方程的正的近似根是( )
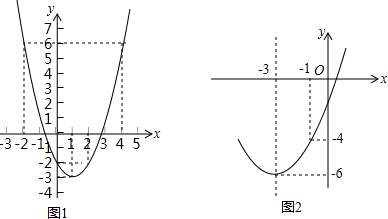
| x | -0.9 | -0.8 | -0.7 | -0.6 |
| y=x2-2x-2 | -0.61 | 0.24 | -0.11 | -0.44 |

| A. | 0.7 | B. | 2.6 | C. | 2.7 | D. | 2.8 |
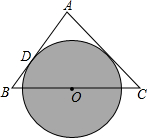 如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)
如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)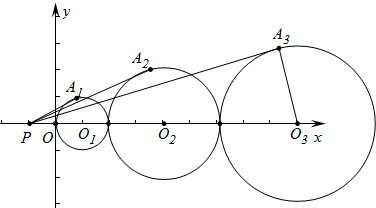 如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.
如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.