题目内容
12.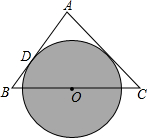 如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)
如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)
分析 连接OD、AO,作OE⊥AC于E,只要证明OE=OD即可.
解答 证明: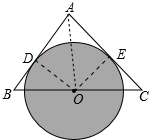 连接OD、AO,作OE⊥AC于E.
连接OD、AO,作OE⊥AC于E.
∵AB=AC,OB=OC,
∴OA平分∠BAC,
∵AB切⊙O于D,
∴OD⊥AB,
∵OE⊥AC,
∴OD=OE,
∴AC是⊙O的切线.
点评 本题考查切线的判定和性质、等腰三角形的性质、角平分线的性质等知识,解题的关键是熟练掌握切线的两种判定方法①过半径的外端垂直半径的直线是圆的切线②圆心到直线的距离等于半径,这条直线是圆的切线,学会添加辅助线的方法,属于中考常考题型.

练习册系列答案
相关题目
3.计算$\sqrt{12}$÷$\sqrt{\frac{27}{2}}$×$\sqrt{\frac{1}{36}}$的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{9}$ | D. | $\frac{3}{2}$ |
20.如图是某实物的三视图,则这个实物是( )


| A. |  | B. |  | C. |  | D. |  |
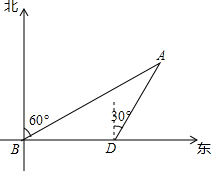 如图,海中有一小岛A,它的周围10海里内有暗礁,渔船由西向东航行.在B点测得小岛A在北偏东60°方向,再航行12海里到达D点,这时测得小岛A在北偏东30°方向.如果渔船不改变航向,继续向东航行,有没有触礁的危险?
如图,海中有一小岛A,它的周围10海里内有暗礁,渔船由西向东航行.在B点测得小岛A在北偏东60°方向,再航行12海里到达D点,这时测得小岛A在北偏东30°方向.如果渔船不改变航向,继续向东航行,有没有触礁的危险?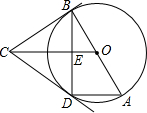 如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.
如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.