题目内容
1.如果$\sqrt{a-5}$+|b-3|=0,求以a,b为边长的等腰三角形的周长.分析 先根据非负数的性质得到a、b的长,再分为两种情况:①当腰是2,底边是3时,②当腰是3,底边是2时,求出即可.
解答 解:∵$\sqrt{a-5}$+|b-3|=0,
∴a-5=0,b-3=0,
解得a=5,b=3,
①当腰是5,底边是3时,三边长是5,5,3,此时符合三角形的三边关系定理,
即等腰三角形的周长是5+5+3=13;
②当腰是3,底边是5时,三边长是3,3,5,此时符合三角形的三边关系定理,
即等腰三角形的周长是3+3+5=11.
∴等腰三角形的周长为13或11.
点评 本题考查了非负数的性质、等腰三角形的性质和三角形的三边关系定理的应用,注意此题要分为两种情况讨论.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
6.下列同类二次根式合并过程正确的是( )
| A. | 2$\sqrt{3}$-$\sqrt{3}$=2 | B. | a$\sqrt{c}$+b$\sqrt{c}$=a+b$\sqrt{c}$ | C. | 5$\sqrt{a}$+$\frac{1}{2}$$\sqrt{a}$=5+$\frac{1}{2}$$\sqrt{a}$ | D. | $\frac{1}{3}$$\sqrt{3a}$-$\frac{1}{4}$$\sqrt{3a}$=$\frac{1}{12}$$\sqrt{3a}$ |
9.化简$\frac{x-y}{\sqrt{x}+\sqrt{y}}$,甲、乙两位同学的解法如下:
甲:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$=$\sqrt{x}$-$\sqrt{y}$;
乙:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$.
对于甲、乙两位同学的解法,正确的判断是( )
甲:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$=$\sqrt{x}$-$\sqrt{y}$;
乙:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$.
对于甲、乙两位同学的解法,正确的判断是( )
| A. | 甲、乙都正确 | B. | 甲正确,乙不正确 | C. | 甲、乙都不正确 | D. | 乙正确,甲不正确 |
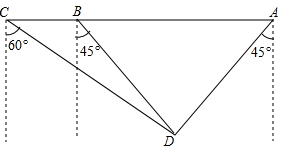 如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)
如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)