题目内容
8.我们来看一个这样的例子,分母有理化:$\frac{1}{\sqrt{2}-1}$=$\frac{\sqrt{2}+1}{(\sqrt{2}-1)•(\sqrt{2}+1)}$=$\frac{\sqrt{2}+1}{(\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{2}$+1.
比较大小:$\sqrt{6}$-$\sqrt{5}$和$\sqrt{3}$-$\sqrt{2}$.
分析 先求出每个式子的倒数,根据倒数即可比较两数的大小.
解答 解:$\frac{1}{\sqrt{6}-\sqrt{5}}$=$\frac{\sqrt{6}+\sqrt{5}}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}$=$\frac{\sqrt{6}+\sqrt{5}}{(\sqrt{6})^{2}-(\sqrt{5})^{2}}$=$\sqrt{6}$+$\sqrt{5}$.$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=$\sqrt{3}$+$\sqrt{2}$.
∵$\sqrt{6}$+$\sqrt{5}$>$\sqrt{3}$+$\sqrt{2}$>0,$\frac{1}{\sqrt{6}-\sqrt{5}}$>$\frac{1}{\sqrt{3}-\sqrt{2}}$>0,
∴$\sqrt{6}$-$\sqrt{5}$<$\sqrt{3}$-$\sqrt{2}$.
点评 本题考查了二次根式的性质,分母有理化,实数的大小比较等知识点,主要考查学生能否选择适当的方法比较两实数的大小,题目比较好.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
3.计算$\sqrt{12}$÷$\sqrt{\frac{27}{2}}$×$\sqrt{\frac{1}{36}}$的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{9}$ | D. | $\frac{3}{2}$ |
20.如图是某实物的三视图,则这个实物是( )


| A. |  | B. |  | C. |  | D. |  |
 B.
B.  C. -5 D. 5
C. -5 D. 5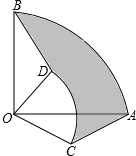 把两个圆心角都是90°的扇形OAB与扇形OCD按如图所示位置叠放在一起,连接AC,BD.
把两个圆心角都是90°的扇形OAB与扇形OCD按如图所示位置叠放在一起,连接AC,BD.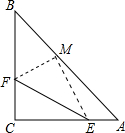 如图,△ABC中,CA=CB,∠ACB=90°,E、F分别在CA、CB上,将△CEF沿直线EF翻折,点C恰好落在AB上的点M处,若AM=3BM,求$\frac{CF}{CE}$.
如图,△ABC中,CA=CB,∠ACB=90°,E、F分别在CA、CB上,将△CEF沿直线EF翻折,点C恰好落在AB上的点M处,若AM=3BM,求$\frac{CF}{CE}$.