题目内容
4.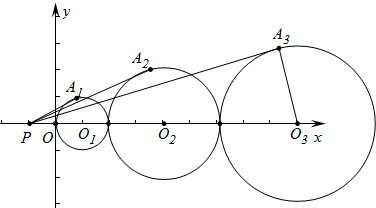 如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.
如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.
分析 在RT△PA3O3,根据三角函数的定义即可解决问题.
解答  解:如图,连接PA3,
解:如图,连接PA3,
∵PA3是⊙O3的切线,
∴PA3⊥O3A3,
∴∠PA3O3=90°,
在RT△PA3O3中,∵∠PA3O3=90°,A3O3=3,PO3=10,
∴sin∠A3PO3=$\frac{{A}_{3}{O}_{3}}{P{O}_{3}}$=$\frac{3}{10}$.
故答案为$\frac{3}{10}$.
点评 本题考查切线的性质、三角函数的定义,熟练应用切线的性质以及三角函数的定义是解题的关键,属于中考常考题型.

练习册系列答案
相关题目
9.化简$\frac{x-y}{\sqrt{x}+\sqrt{y}}$,甲、乙两位同学的解法如下:
甲:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$=$\sqrt{x}$-$\sqrt{y}$;
乙:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$.
对于甲、乙两位同学的解法,正确的判断是( )
甲:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$=$\sqrt{x}$-$\sqrt{y}$;
乙:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$.
对于甲、乙两位同学的解法,正确的判断是( )
| A. | 甲、乙都正确 | B. | 甲正确,乙不正确 | C. | 甲、乙都不正确 | D. | 乙正确,甲不正确 |
13.下列各图中,能够由∠1=∠2得到AB∥CD的是( )
| A. | 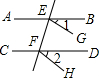 | B. | 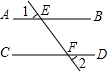 | C. | 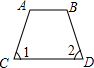 | D. |  |
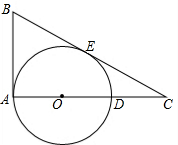 如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.
如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.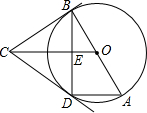 如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.
如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.