题目内容
17.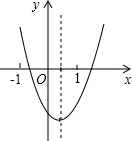 二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )
二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由抛物线的开口方向可确定a的符号,由抛物线的对称轴相对于y轴的位置可得a与b之间的符号关系,由抛物线与y轴的交点位置可确定c的符号;由抛物线与x轴交点个数可确定b2-4ac的符号;根据抛物线的对称轴与x=1的大小关系可推出2a+b的符号;由于x=1时y=a+b+c,因而结合图象,可根据x=1时y的符号来确定a+b+c的符号.
解答 解:由抛物线的开口向上可得a>0,
由抛物线的对称轴在y轴的右边可得x=-$\frac{b}{2a}$>0,则a与b异号,因而b<0,
由抛物线与y轴的交点在y轴的负半轴上可得c<0,
∴abc>0;
由抛物线与x轴有两个交点可得b2-4ac>0;
由抛物线的对称轴x=-$\frac{b}{2a}$<1(a>0),可得-b<2a,即2a+b>0;
由x=1时y<0可得a+b+c<0.
综上所述:abc,b2-4ac,2a+b这三个式子的值为正数.
故选B.
点评 本题主要考查二次函数图象与系数的关系,其中a决定于抛物线的开口方向,b决定于抛物线的开口方向及抛物线的对称轴相对于y轴的位置,c决定于抛物线与y轴的交点位置,b2-4ac的符号决定于抛物线与x轴交点个数,2a+b的符号决定于a的符号及-$\frac{b}{2a}$与1的大小关系,运用数形结合的思想准确获取相关信息是解决本题的关键.

练习册系列答案
相关题目
 已知:如图,CD是Rt△ABC的斜边AB上的高,用余弦、正切的定义证明:
已知:如图,CD是Rt△ABC的斜边AB上的高,用余弦、正切的定义证明: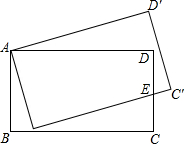 如图所示,将矩形ABCD旋转到AB′C′D′位置,使边BC恰好经过边CD的中点E.若AB=8,C′E=2,则四边形AB′ED的面积是70.
如图所示,将矩形ABCD旋转到AB′C′D′位置,使边BC恰好经过边CD的中点E.若AB=8,C′E=2,则四边形AB′ED的面积是70.
 如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.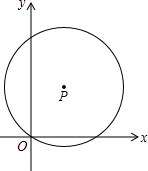 如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.
如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.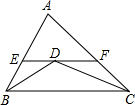 如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过D作直线平行于BC,交AB、AC于E、F,若BE+CF=7.则EF=( )
如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过D作直线平行于BC,交AB、AC于E、F,若BE+CF=7.则EF=( )