题目内容
10. 已知:如图,CD是Rt△ABC的斜边AB上的高,用余弦、正切的定义证明:
已知:如图,CD是Rt△ABC的斜边AB上的高,用余弦、正切的定义证明:(1)BC2=AB•BD;
(2)CD2=AD•BD.
分析 (1)根据余弦的定义,分别在Rt△ABC和Rt△DBC中表示出cosB,根据等式的性质计算即可;
(2)证明∠ACD=∠B,根据∠ACD和∠B的正切值相等计算.
解答 解:(1)∵CD是Rt△ABC的斜边AB上的高,
∴∠ACB=∠CDB=90°,
在Rt△ABC中,
cosB=$\frac{BC}{AB}$,
在Rt△DBC中,
cosB=$\frac{BD}{BC}$,
∴$\frac{BC}{AB}$=$\frac{BD}{BC}$,即BC2=AB•BD;
(2)∵∠ACB=∠CDB=90°,
∴∠ACD=∠B,
在Rt△ADC中,
tan∠ACD=$\frac{AD}{CD}$,
在Rt△DBC中,
tanB=$\frac{CD}{BD}$,
∴$\frac{AD}{CD}$=$\frac{CD}{BD}$,即CD2=AD•BD.
点评 本题考查的是锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
17.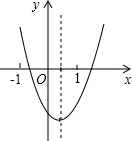 二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )
二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )
 二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )
二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
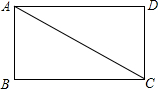 已知:如图,Rt△ABC≌Rt△CDA,其中点A,D的对应点分别是C,B,∠B=∠D=Rt∠.求证:四边形ABCD是矩形.
已知:如图,Rt△ABC≌Rt△CDA,其中点A,D的对应点分别是C,B,∠B=∠D=Rt∠.求证:四边形ABCD是矩形.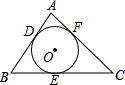 如图所示,⊙O分别切△ABC的三边AB、BC、CA于点D、E、F,若BC=10,AC=11,AB=8,求AF、BD、CE的长.
如图所示,⊙O分别切△ABC的三边AB、BC、CA于点D、E、F,若BC=10,AC=11,AB=8,求AF、BD、CE的长.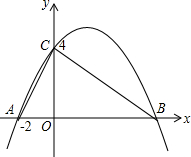 如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过Rt△ABC的三个顶点,其中∠ACB=90°,点A坐标为(-2,0),点C的坐标为(0,4).
如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过Rt△ABC的三个顶点,其中∠ACB=90°,点A坐标为(-2,0),点C的坐标为(0,4).