题目内容
8.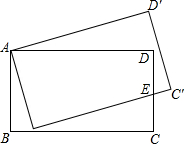 如图所示,将矩形ABCD旋转到AB′C′D′位置,使边BC恰好经过边CD的中点E.若AB=8,C′E=2,则四边形AB′ED的面积是70.
如图所示,将矩形ABCD旋转到AB′C′D′位置,使边BC恰好经过边CD的中点E.若AB=8,C′E=2,则四边形AB′ED的面积是70.
分析 设AD=x,则B′E=x-2,连接AE,在直角△AB'E中利用勾股定理即可列方程求得x的值,然后根据四边形AB′ED的面积等于△AB'E和△ADE的面积的和求解.
解答  解:设AD=x,则B'E=x-2,连接AE.
解:设AD=x,则B'E=x-2,连接AE.
在直角△AB′E中,AB′2+BE2=AD2+DE2,
则82+(x-2)2=x2+42,
解得:x=13,
则S=$\frac{1}{2}$×13×4+$\frac{1}{2}$×8×(13-2)=26+44=70.
故答案是:70.
点评 本题考查了图形的旋转和勾股定理的应用,在直角△AB'E中利用勾股定理即可列方程求得x的值是关键.

练习册系列答案
相关题目
17.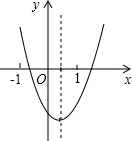 二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )
二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )
 二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )
二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
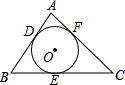 如图所示,⊙O分别切△ABC的三边AB、BC、CA于点D、E、F,若BC=10,AC=11,AB=8,求AF、BD、CE的长.
如图所示,⊙O分别切△ABC的三边AB、BC、CA于点D、E、F,若BC=10,AC=11,AB=8,求AF、BD、CE的长.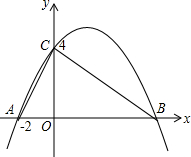 如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过Rt△ABC的三个顶点,其中∠ACB=90°,点A坐标为(-2,0),点C的坐标为(0,4).
如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过Rt△ABC的三个顶点,其中∠ACB=90°,点A坐标为(-2,0),点C的坐标为(0,4).
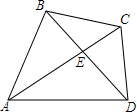 四边形ABCD中,对角线AC平分∠BAD,且满足∠BAD+∠BCD=180°,求证:$\frac{CB}{CE}$=$\frac{CA}{CB}$.
四边形ABCD中,对角线AC平分∠BAD,且满足∠BAD+∠BCD=180°,求证:$\frac{CB}{CE}$=$\frac{CA}{CB}$.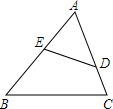 如图,D、E分别是△ABC的边AC、AB上的点,AD=6,AB=10,BC=12,且$\frac{AE}{AC}=\frac{3}{5}$,
如图,D、E分别是△ABC的边AC、AB上的点,AD=6,AB=10,BC=12,且$\frac{AE}{AC}=\frac{3}{5}$, 如图,梯形ABCD中,AD∥BC,AC⊥BC,且∠D=∠BAC.求证:AC2=AD•BC.
如图,梯形ABCD中,AD∥BC,AC⊥BC,且∠D=∠BAC.求证:AC2=AD•BC.