题目内容
9.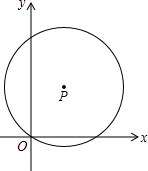 如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.
如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.(1)若b=5,则点A坐标是(0,10);
(2)在(1)的条件下,若OQ=8,求线段BQ的长;
(3)若点P在函数y=x2(x>0)的图象上,△BQP是等腰三角形且PQ=$\sqrt{10}$,求出点B的坐标.
分析 (1)过点P作PH⊥OA于点H,由垂径定理可求出OA的长,进而可求出A的坐标;
(2)连接BP、OP,由已知条件易求QH,在Rt△QHP中,由勾股定理可得:PQ2=QH2+PH2=9+PH2,在Rt△PHO中,由勾股定理可得:PO2=OH2+PH2=25+PH2=BP2,进而在Rt△BQP中,BQ2=BP2-PQ2=(25+PH2)-(9+PH2)=16.所以BQ=4;
(3)作BM⊥y轴于点M,首先求出a=2,再求出MQ=PH=2,利用勾股定理可求出MB=QH=$\sqrt{6}$.所以可得:B1($\sqrt{6}$,6+$\sqrt{6}$),若点Q在OH上,再由抛物线对称性可得B2($\sqrt{6}$,2-$\sqrt{6}$).
解答  解:(1)过点P作PH⊥OA于点H,
解:(1)过点P作PH⊥OA于点H,
∴OA=2OH,
∵b=5,
∴OH=5,
∴OA=10,
∴点A坐标是(0,10).
故答案为:(0,10).
(2)连接BP、OP.
∵b=5,PH⊥OA,
∴OH=AH=5.
∵OQ=8,
∴QH=OQ-OH=3.
在Rt△QHP中,PQ2=QH2+PH2=9+PH2,
在Rt△PHO中,PO2=OH2+PH2=25+PH2=BP2,
在Rt△BQP中,BQ2=BP2-PQ2=(25+PH2)-(9+PH2)=16.
∴BQ=4;
(3)△BQP是等腰直角三角形,PQ=$\sqrt{10}$,
∴半径BP=2$\sqrt{5}$.
又∵P(a,a2),
∴OP2=a2+a4=(2$\sqrt{5}$)2.
即a4+a2-20=0.
解得a=±2.
∵a>0
∴a=2.
∴P(2,4).
如图,作BM⊥y轴于点M,则△QBM≌△PQH.
∴MQ=PH=2,
∴MB=QH=$\sqrt{P{Q}^{2}-P{H}^{2}}$=$\sqrt{6}$.
∴B1($\sqrt{6}$,6+$\sqrt{6}$).
若点Q在OH上,由对称性可得B2($\sqrt{6}$,2-$\sqrt{6}$)
综上,当PQ=$\sqrt{10}$时,B点坐标为($\sqrt{6}$,6+$\sqrt{6}$)或($\sqrt{6}$,2-$\sqrt{6}$).
点评 本题着重考查了待定系数法求二次函数解析式、勾股定理的运用,三角形全等、探究等腰三角形的构成情况等重要知识点,综合性强,能力要求极高.考查学生分类讨论,数形结合的数学思想方法.

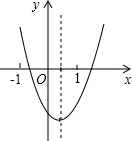 二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )
二次函数y=ax2+bx+c的图象如图所示,则abc,b2-4ac,2a+b,a+b+c这四个式子中,值为正数的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
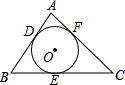 如图所示,⊙O分别切△ABC的三边AB、BC、CA于点D、E、F,若BC=10,AC=11,AB=8,求AF、BD、CE的长.
如图所示,⊙O分别切△ABC的三边AB、BC、CA于点D、E、F,若BC=10,AC=11,AB=8,求AF、BD、CE的长.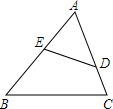 如图,D、E分别是△ABC的边AC、AB上的点,AD=6,AB=10,BC=12,且$\frac{AE}{AC}=\frac{3}{5}$,
如图,D、E分别是△ABC的边AC、AB上的点,AD=6,AB=10,BC=12,且$\frac{AE}{AC}=\frac{3}{5}$,
 如图,梯形ABCD中,AD∥BC,AC⊥BC,且∠D=∠BAC.求证:AC2=AD•BC.
如图,梯形ABCD中,AD∥BC,AC⊥BC,且∠D=∠BAC.求证:AC2=AD•BC.