题目内容
将下列推理补充完整:

(1)如图1:因为∠1=∠2(已知)
所以 ∥ ( )
因为∠1=∠3(已知)
所以 ∥ ( )
因为 EF∥BD(已知)
所以∠3+∠4=180°( )
(2)如图2,已知AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD.( )
∵EG平分∠AEF,FH平分∠EFD.(已知)
∴∠1=
∠AEF,∠2=
∠EFD,( )
∴∠1=∠2( )
∴ ∥ ( )

(1)如图1:因为∠1=∠2(已知)
所以
因为∠1=∠3(已知)
所以
因为 EF∥BD(已知)
所以∠3+∠4=180°(
(2)如图2,已知AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD.(
∵EG平分∠AEF,FH平分∠EFD.(已知)
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2(
∴
考点:平行线的判定与性质
专题:推理填空题
分析:(1)根据平行线的性质和判定方法分别填空即可;
(2)根据平行线的性质,角平分线的定义以及平行线的判定方法分别填空即可.
(2)根据平行线的性质,角平分线的定义以及平行线的判定方法分别填空即可.
解答:解:(1)如图1:因为∠1=∠2(已知)
所以EF∥DB (同位角相等,两直线平行)
因为∠1=∠3(已知)
所以AB∥CD (内错角相等,两直线平行)
因为 EF∥BD(已知)
所以∠3+∠4=180°(两直线平行,同旁内角互补);
(2)如图2,已知AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD.(两直线平行,内错角相等)
∵EG平分∠AEF,FH平分∠EFD.(已知)
∴∠1=
∠AEF,∠2=
∠EFD,(角平分线定义)
∴∠1=∠2(等量代换)
∴GE∥HF(内错角相等,两直线平行)
故答案为:(1)EF,DB,同位角相等,两直线平行;AB,CD,内错角相等,两直线平行;两直线平行,同旁内角互补;
(2)两直线平行,内错角相等;角平分线定义;等量代换;GE,HF,内错角相等,两直线平行.
所以EF∥DB (同位角相等,两直线平行)
因为∠1=∠3(已知)
所以AB∥CD (内错角相等,两直线平行)
因为 EF∥BD(已知)
所以∠3+∠4=180°(两直线平行,同旁内角互补);
(2)如图2,已知AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD.(两直线平行,内错角相等)
∵EG平分∠AEF,FH平分∠EFD.(已知)
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2(等量代换)
∴GE∥HF(内错角相等,两直线平行)
故答案为:(1)EF,DB,同位角相等,两直线平行;AB,CD,内错角相等,两直线平行;两直线平行,同旁内角互补;
(2)两直线平行,内错角相等;角平分线定义;等量代换;GE,HF,内错角相等,两直线平行.
点评:本题考查了平行线的判定与性质,角平分线的定义,主要是对逻辑推理能力的训练,熟记平行线的性质与判定方法是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
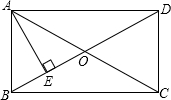 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE=
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE=
 线段HB上一动点,以E为圆心,EA为半径作⊙E,⊙E与线段DC相交于点F,设AE=x,DF=y,
线段HB上一动点,以E为圆心,EA为半径作⊙E,⊙E与线段DC相交于点F,设AE=x,DF=y,