题目内容
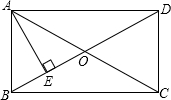 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE=2
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE=2| 3 |
考点:矩形的性质,等边三角形的判定与性质
专题:几何图形问题
分析:根据矩形的对角线相等互相平分可得OB=OD,然后求出OE=BE,然后判断出△ABO是等边三角形,再根据等边三角形的性质求出边长AB即OB的长,然后根据BD=2OB计算即可得解.
解答:解:在矩形ABCD中,OB=OD,
∵ED=3OE,
∴OE=BE,
∴AE垂直平分OB,
∴AB=AO,
又∵OA=OB,
∴△ABO是等边三角形,
∵AE=2
,
∴OB=AB=2
÷
=4,
∴BD=2OB=2×4=8.
∵ED=3OE,
∴OE=BE,
∴AE垂直平分OB,
∴AB=AO,
又∵OA=OB,
∴△ABO是等边三角形,
∵AE=2
| 3 |
∴OB=AB=2
| 3 |
| ||
| 2 |
∴BD=2OB=2×4=8.
点评:本题考查了矩形的性质,等边三角形的判定与性质,主要利用了矩形的对角线相等且互相平分的性质,熟记性质是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,以点O为圆心,OB为半径画弧,交数轴于点A,若点A所表示的数为x,则x的值为( )
如图,以点O为圆心,OB为半径画弧,交数轴于点A,若点A所表示的数为x,则x的值为( )A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
关于函数y=kx+b(k,b都是不等于0的常数),下列说法,正确的是( )
| A、y与x成正比例 |
| B、y与kx成正比例 |
| C、y与x+b成正比例 |
| D、y-b与x成正比例 |
若等腰三角形的周长为60厘米,底边长为y厘米,一腰长为x厘米,则y与x的函数关系式及自变量x的取值范围是( )
| A、y=60-2x(0<x<30) | ||
| B、y=60-2x(15<x<30) | ||
C、y=
| ||
D、y=
|
 如图,将△ABC的边BC沿射线BA方向平移,距离为线段AB的长,得到线段AD;再将边AB沿BC方向平移,平移的距离为线段BC的长,得到线段CE,试问:
如图,将△ABC的边BC沿射线BA方向平移,距离为线段AB的长,得到线段AD;再将边AB沿BC方向平移,平移的距离为线段BC的长,得到线段CE,试问: 如图,设二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于C点,若AO=20,OB=15,∠ACB=90°,求这个二次函数的解析式.
如图,设二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于C点,若AO=20,OB=15,∠ACB=90°,求这个二次函数的解析式.