题目内容
20. 如图,点C在线段AD上,AB∥DE,AC=DE,AB=CD,CF平分∠BCE,试探究CF和BE的位置关系,并说明理由.
如图,点C在线段AD上,AB∥DE,AC=DE,AB=CD,CF平分∠BCE,试探究CF和BE的位置关系,并说明理由.
分析 由条件可证明△ABC≌△DCE,可得CE=CB,再利用等腰三角形的性质可求利CF⊥BE.
解答 解:CF⊥BE.
理由如下:
∵AB∥DE,
∴∠A=∠D,
在△ABC和△DCE中
$\left\{\begin{array}{l}{AB=CD}\\{∠A=∠D}\\{AC=DE}\end{array}\right.$
∴△ABC≌△DCE(SAS),
∴CE=CB,
∵CF平分∠BCE,
∴CF⊥BE.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
9.已知点A(a,-b)在第二象限,则点B(a-3,b-2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |




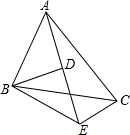 如图,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$,且∠CBE=25°,求∠ABD的度数.
如图,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$,且∠CBE=25°,求∠ABD的度数. 如图,长方体的长、宽、高分别是9cm,7cm,8cm,一只蚂蚁沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短路径长$\sqrt{296}$.
如图,长方体的长、宽、高分别是9cm,7cm,8cm,一只蚂蚁沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短路径长$\sqrt{296}$.