题目内容
9．已知点A（a，-b）在第二象限，则点B（a-3，b-2）在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 根据第二象限内点的横坐标小于零，纵坐标大于零，可得a、b的范围，根据不等式的性质，可得a-3，b-2，根据第三象限内点的横坐标小于零，纵坐标小于零，可得答案．
解答 解：由A（a，-b）在第二象限，得
a＜0，-b＞0．
由不等式的性质，得
a-3＜-3，b＜0．
b-2＜-2，
点B（a-3，b-2）在第三象限，
故选：C．
点评 本题考查了点的坐标，熟记各象限内点的坐标特征是解题关键．
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
如图，点C在线段AD上，AB∥DE，AC=DE，AB=CD，CF平分∠BCE，试探究CF和BE的位置关系，并说明理由．
17．
如图，有理数a，b，c，d在数轴上的对应点分别是A，B，C，D，若a+c=0，则b+d（ ）
如图，有理数a，b，c，d在数轴上的对应点分别是A，B，C，D，若a+c=0，则b+d（ ）| A． | 大于0 | B． | 小于0 | C． | 等于0 | D． | 不确定 |
4．下列运算正确的是（ ）
| A． | $\sqrt{36}$=±6 | B． | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C． | $\sqrt{12}$÷$\sqrt{2}$=6 | D． | $\sqrt{\frac{3}{2}}$×$\sqrt{24}$=6 |
若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是（ ）
1．
如图，在?ABCD中，若∠A+∠C=130°，则∠D的大小为（ ）
如图，在?ABCD中，若∠A+∠C=130°，则∠D的大小为（ ）| A． | 100° | B． | 105° | C． | 110° | D． | 115° |
18．
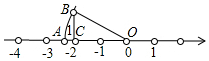已知，如图，OA=OB，那么数轴上的点A所表示的数是（ ）
已知，如图，OA=OB，那么数轴上的点A所表示的数是（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | -$\sqrt{5}$ | D． | -$\sqrt{7}$ |
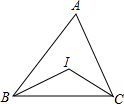如图，△ABC中，∠A=45°，I是内心，则∠BIC=115°．