Question

11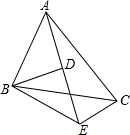．如图，$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$，且∠CBE=25°，求∠ABD的度数．

Answer 1

分析 先利用三组对应边成比例的两三角形相似判断△ABC∽△DBE，则∠ABC=∠DBE，于是得到∠ABD=∠CBE=25°．

解答 解：∵$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$，
∴△ABC∽△DBE，
∴∠ABC=∠DBE，
∴∠ABC-∠ABD=∠DBC-∠CBE，
∴∠ABD=∠CBE=25°．

点评 本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在利用三角形相似的性质时，主要得到对应角相等，对应边成比例．