题目内容
8. 如图,长方体的长、宽、高分别是9cm,7cm,8cm,一只蚂蚁沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短路径长$\sqrt{296}$.
如图,长方体的长、宽、高分别是9cm,7cm,8cm,一只蚂蚁沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短路径长$\sqrt{296}$.
分析 蚂蚁有三种爬法,就是把正视和俯视(或正视和侧视,或俯视和侧视)二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短的途径.
解答  解:如图所示,
解:如图所示,
路径一:AB=$\sqrt{(7+9)^{2}+{8}^{2}}$=8$\sqrt{5}$;
路径二:AB=$\sqrt{(8+7)^{2}+{9}^{2}}$=$\sqrt{296}$;
路径三:AB=$\sqrt{(8+9)^{2}+{7}^{2}}$=$\sqrt{305}$;
∵$\sqrt{320}$>$\sqrt{305}$>$\sqrt{296}$,
∴$\sqrt{296}$cm为最短路径.
故答案为$\sqrt{296}$.
点评 本题考查了平面展开---最短路径问题,解题的关键是将图形展开,转化为直角三角形利用勾股定理解答.

练习册系列答案
相关题目
17. 如图,有理数a,b,c,d在数轴上的对应点分别是A,B,C,D,若a+c=0,则b+d( )
如图,有理数a,b,c,d在数轴上的对应点分别是A,B,C,D,若a+c=0,则b+d( )
 如图,有理数a,b,c,d在数轴上的对应点分别是A,B,C,D,若a+c=0,则b+d( )
如图,有理数a,b,c,d在数轴上的对应点分别是A,B,C,D,若a+c=0,则b+d( )| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 不确定 |
18.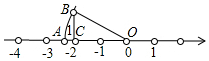 已知,如图,OA=OB,那么数轴上的点A所表示的数是( )
已知,如图,OA=OB,那么数轴上的点A所表示的数是( )
 已知,如图,OA=OB,那么数轴上的点A所表示的数是( )
已知,如图,OA=OB,那么数轴上的点A所表示的数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | -$\sqrt{7}$ |
 已知有理数a、b在数轴上表示的点如图,用“<”把a、b、-a、-b的大小连接起来a<-b<b<-a.
已知有理数a、b在数轴上表示的点如图,用“<”把a、b、-a、-b的大小连接起来a<-b<b<-a. 如图,Rt△ABC的角平分线AD与BE相交于F,M是DE的中点,设FM=2.5,S△DEF=15,求CD,AB的长.
如图,Rt△ABC的角平分线AD与BE相交于F,M是DE的中点,设FM=2.5,S△DEF=15,求CD,AB的长. 如图,点C在线段AD上,AB∥DE,AC=DE,AB=CD,CF平分∠BCE,试探究CF和BE的位置关系,并说明理由.
如图,点C在线段AD上,AB∥DE,AC=DE,AB=CD,CF平分∠BCE,试探究CF和BE的位置关系,并说明理由.