题目内容
10.在半径为1cm,圆心角是90°的扇形的内部挖去一个最大的圆,则余下的图形的面积为$\frac{8\sqrt{2}-11}{4}$π.分析 显然当小圆与扇形的两半径及弧相切时小圆最大,设小圆半径为r,继而根据OP+PF=1可得关于r的方程,解之可得r,再用扇形面积减去圆的面积即可得.
解答 解:如图,设⊙P的半径为r,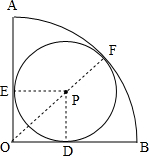
∴PD=PE=PF=r,
∵∠PEO=∠AOB=∠PDO=90°,
∴四边新PEOD为正方形,
∴PO=$\sqrt{2}$PE=$\sqrt{2}$r,
∴OF=OP+PF=$\sqrt{2}$r+r=1,
解得:r=$\sqrt{2}$-1,
则余下的图形的面积为$\frac{1}{4}$×π×12-π•($\sqrt{2}$-1)2=$\frac{8\sqrt{2}-11}{4}$π,
故答案为:$\frac{8\sqrt{2}-11}{4}$π.
点评 本题主要考查扇形面积的计算,根据题意求得内部最大圆的半径是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
1. 如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )
如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )
 如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )
如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )| A. | 100° | B. | 105° | C. | 110° | D. | 115° |
18.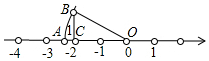 已知,如图,OA=OB,那么数轴上的点A所表示的数是( )
已知,如图,OA=OB,那么数轴上的点A所表示的数是( )
 已知,如图,OA=OB,那么数轴上的点A所表示的数是( )
已知,如图,OA=OB,那么数轴上的点A所表示的数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | -$\sqrt{7}$ |
5.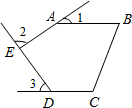 如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
 如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )| A. | 90° | B. | 180° | C. | 120° | D. | 270° |
 如图,点C在线段AD上,AB∥DE,AC=DE,AB=CD,CF平分∠BCE,试探究CF和BE的位置关系,并说明理由.
如图,点C在线段AD上,AB∥DE,AC=DE,AB=CD,CF平分∠BCE,试探究CF和BE的位置关系,并说明理由.
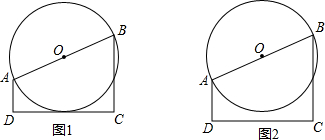
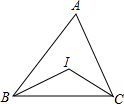 如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°.
如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°. 如图是一台水泵的叶轮平面示意图,它绕着圆心O旋转最小度数为45°后可以与自身重合.
如图是一台水泵的叶轮平面示意图,它绕着圆心O旋转最小度数为45°后可以与自身重合.