题目内容
4.如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC=8,CB=6,求线段MN的长;
(2)若点C为线段AB上任意一点,且满足AC+BC=a,请直接写出线段MN的长;
(3)若点C为线段AB延长线上任意一点,且满足AC-CB=b,求线段MN的长.
分析 (1)由M、N分别是AC、BC的中点,于是得到MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$CB,即可求得结论;
(2)由M、N分别是线段AC、BC的中点,于是得到AM=MC,CN=BN,求得AM+CM+CN+NB=a,于是得到结果;
(3)由M、N分别是AC、BC的中点,得到MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,即可得到结论.
解答 解:(1)∵M、N分别是AC、BC的中点,
∴MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$CB,
∴MN=MC+CN,
=$\frac{1}{2}$( AC+CB)
=$\frac{1}{2}$(8+6)
=7;
(2)∵若M、N分别是线段AC、BC的中点,
∴AM=MC,CN=BN,
AM+CM+CN+NB=a,
2(CM+CN)=a,
CM+CN=$\frac{a}{2}$,
∴MN=$\frac{1}{2}$a;
(3)∵M、N分别是AC、BC的中点,
∴MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,
∴MN=MC-NC
=$\frac{1}{2}$(AC-BC)
=$\frac{1}{2}$b.
点评 本题考查了两点间的距离,利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.

练习册系列答案
相关题目
19.小王利用计算机设计了一个计算程序,输入和输出的数据如表:那么,当输入数据为8时,输出的数据为( )
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{4}{17}$ | $\frac{5}{26}$ | … |
| A. | $\frac{8}{61}$ | B. | $\frac{1}{62}$ | C. | $\frac{8}{63}$ | D. | $\frac{8}{65}$ |
9.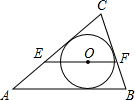 如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
 如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )| A. | EF>AE+BF | B. | EF<AE+BF | C. | EF2=AE•BF | D. | EF=AE+BF |

 已知点C是线段AB延长线上一点,M为AC的中点,N为BC的中点,若AB=8,求MN的长.
已知点C是线段AB延长线上一点,M为AC的中点,N为BC的中点,若AB=8,求MN的长.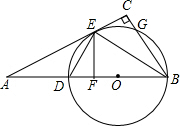 如图,在△ABC中,∠C=90°,BE是∠ABC的平分线,过点E作BE的垂线交AB于点F,⊙O是△BDE的外接圆.求证:
如图,在△ABC中,∠C=90°,BE是∠ABC的平分线,过点E作BE的垂线交AB于点F,⊙O是△BDE的外接圆.求证: