题目内容
13.现有5个边长为1的小正方形如图④所示,请在图④中画出合适的分割线,使分割后的部分能拼成一个新正方形,并把拼图画在图⑤的正方形网格(图中每个小正方形的边长为1)中(直接画出图形,不要求写分析过程),则图⑤中所拼成的新正方形的边长为$\sqrt{5}$.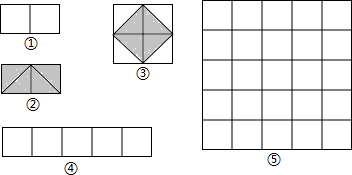
分析 设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得x=$\sqrt{5}$,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图④所示的分割线,拼出如图⑤所示的新正方形.
解答 解:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,
x2=5,解得:x=$\sqrt{5}$,
所以拼成的新正方形的边长为$\sqrt{5}$.
如图,
点评 此题考查图形的剪拼,勾股定理,正方形的面积,掌握勾股定理和正方形的面积是解决问题的关键.

练习册系列答案
相关题目
8.若线段AB=BC+AC,则关于点C正确的是( )
| A. | C是AB的中点 | |
| B. | C不是AB的中点 | |
| C. | C不是AB的中点,A,B,C不共线 | |
| D. | C不一定是AB的中点,A,B,C三点共线 |
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠PBC=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠PBC=∠C.
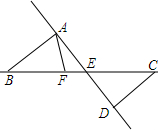 如图,直线AD,BC相交于点E,AB∥CD,F是直线BC上一点(F点与B,E,C三点不重合).
如图,直线AD,BC相交于点E,AB∥CD,F是直线BC上一点(F点与B,E,C三点不重合).