题目内容
一根铝合金型材长为6m,用它制作一个日字型的窗框,如果恰好用完这根铝合金型材,那么窗架的长宽各为多少米时,窗架的面积最大?
考点:二次函数的最值
专题:
分析:设窗架的长为x米,则宽为
米,根据面积公式列出二次函数解析式,根据二次函数的性质即可求解.
| 6-2x |
| 3 |
解答:解:设窗架的长为x米,则宽为
米,
则S=
x,即S=-
x2+2x,
要使窗架的面积最大,
则x=-
=1.5,
于是宽为
=
=1,
所以要使做成的窗架的面积最大,
故该窗的长,宽各为1.5米,1米时,窗架的面积最大.
| 6-2x |
| 3 |
则S=
| 6-2x |
| 3 |
| 2 |
| 3 |
要使窗架的面积最大,
则x=-
| 2 | ||
2×(-
|
于是宽为
| 6-2x |
| 3 |
| 6-2×1.5 |
| 3 |
所以要使做成的窗架的面积最大,
故该窗的长,宽各为1.5米,1米时,窗架的面积最大.
点评:此题考查的是二次函数在实际生活中的运用及求函数最值的方法,属较简单题目.解题的关键是用一个未知数表示出长和宽,利用面积公式来列出函数表达式后再求其最值.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系得到的数学公式是( )
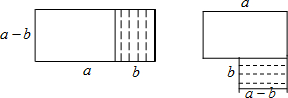

| A、(a+b)(a-b)=a2-b2 |
| B、(a+b)2=a2+2ab+b2 |
| C、(a-b)2=a2-2ab+b2 |
| D、a2-ab=a(a-b) |
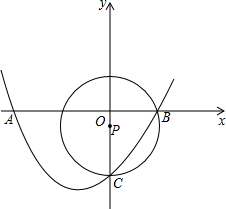 已知:如图,抛物线y=ax2+bx+c(a≠0)经过X轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,-1.5),⊙P的圆心P在y轴上,且经过B、C两点,若b=
已知:如图,抛物线y=ax2+bx+c(a≠0)经过X轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,-1.5),⊙P的圆心P在y轴上,且经过B、C两点,若b=