题目内容
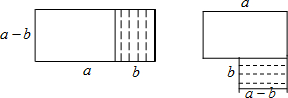
将图甲中阴影部分的小长方形变换到图乙位置，你能根据两个图形的面积关系得到的数学公式是（ ）
| A、（a+b）（a-b）=a2-b2 |
| B、（a+b）2=a2+2ab+b2 |
| C、（a-b）2=a2-2ab+b2 |
| D、a2-ab=a（a-b） |
考点：平方差公式的几何背景
专题：
分析：分别表示两个图形的面积，然后根据两个图形的面积相等，A即可得到答案为：A．
解答：解：左边图形的面积可以表示为：（a+b）（a-b），
右边图形的面积可以表示为：（a-b）b+a（a-b），
∵左边图形的面积=右边图形的面积，
∴（a+b）（a-b）=（a-b）b+a（a-b），
即：（a+b）（a-b）=a2-b2．
故答案为：A．
右边图形的面积可以表示为：（a-b）b+a（a-b），
∵左边图形的面积=右边图形的面积，
∴（a+b）（a-b）=（a-b）b+a（a-b），
即：（a+b）（a-b）=a2-b2．
故答案为：A．
点评：此题考查了平方差公式的几何背景，根据两个图形的面积相等，列等式是解题的关键．
练习册系列答案
相关题目
如图，已知AB、AC是⊙O的弦，AD平分∠BAC交⊙O于D，弦DE∥AB交AC于P，求证：OP平分∠APD．
如图，已知：某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆影长时，因旗杆靠近一幢房子，影子不全落在地面上，有一部分落在墙上，他测得落在地面上的影长为9米，留在墙上的影长CD为2米，求旗杆的高度．
在数轴上表示下列各数，并按从小到大的顺序用“＜”把这些数连结起来．3.5，-3.5，0，2，-2．
如图所示，CZ=