题目内容
求证:等腰三角形的两腰上的高线的交点在顶角的平分线上.
考点:等腰三角形的性质
专题:证明题
分析:根据题意写出已知和求证并作出图形,然后进行证明即可证得此命题正确.
解答: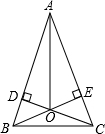 解:已知:△ABC中,AB=AC,BE和CD分别是两腰上的高,
解:已知:△ABC中,AB=AC,BE和CD分别是两腰上的高,
求证:AO平分∠BAC.
证明:∵BE和CD分别是两腰上的高,
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中,
∴△ABE≌△ACD,
∴BE=CD,∠ABE=∠ACD,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EBC=∠DCB,
∴BO=CO,
∴OD=OE,
∴AO平分∠BAC.
 解:已知:△ABC中,AB=AC,BE和CD分别是两腰上的高,
解:已知:△ABC中,AB=AC,BE和CD分别是两腰上的高,求证:AO平分∠BAC.
证明:∵BE和CD分别是两腰上的高,
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中,
|
∴△ABE≌△ACD,
∴BE=CD,∠ABE=∠ACD,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EBC=∠DCB,
∴BO=CO,
∴OD=OE,
∴AO平分∠BAC.
点评:本题考查了等腰三角形的性质,解题的关键是根据题意写出已知、求证并作出图形,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x2-3xy=9,xy-y2=4,则代数式y2-
x2值为( )
| 1 |
| 3 |
| A、-7 | B、1 | C、7 | D、-1 |
 如图,已知:某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆影长时,因旗杆靠近一幢房子,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为9米,留在墙上的影长CD为2米,求旗杆的高度.
如图,已知:某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆影长时,因旗杆靠近一幢房子,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为9米,留在墙上的影长CD为2米,求旗杆的高度.