题目内容
2.我们做如下的规定:如果一个三角形在运动变化时保持形状和大小不变,则把这样的三角形称为三角形板.把两块边长为4的等边三角形板ABC和DEF叠放在一起,使三角形板DEF的顶点D与三角形板ABC的AC边中点O重合,把三角形板ABC固定不动,让三角形板DEF绕点O旋转,设射线DE与射线AB相交于点M,射线DF与线段BC相交于点N.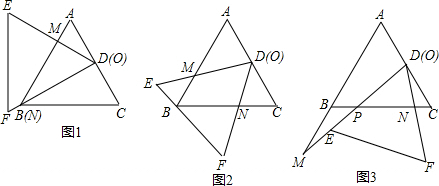
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△ADM∽△CND.此时,AM•CN=4.
(2)将三角形板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AM•CN的值是否改变?说明你的理由.
(3)在(2)的条件下,设AM=x,两块三角形板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
分析 (1)可通过证△ADM∽△CND来求解.
(2)不会改变,关键是还是证△ADM∽△CND,已知一组60°角,关键是证(1)中的∠ADM=∠CND,由于图2由图1旋转而得,根据旋转的性质可设旋转角为α,则∠DNC=∠DBN+∠BDN=30°+α,∠ADM=30°+α,因此两角相等.由此可证得两三角形相似.因此结论不变.
(3)本题分类两种情况进行讨论:①当0°<α<60°时;②当60°≤α<90°时.
解答 解:(1)∵∠A=∠C=∠D=60°,
∴∠ADM+∠CDN=120°,∠ADM+∠AMD=120°,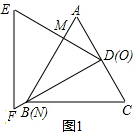
∴∠CDN=∠AMD,
∴△ADM∽△CND,
∴$\frac{AD}{CN}=\frac{AM}{CD}$,
∴AM•CN=AD•CD,
∵顶点D与三角形板ABC的AC边中点O重合,
∴AD=CD=2,
∴AM•CN=AD•CD=2×2=4,
故答案为:4;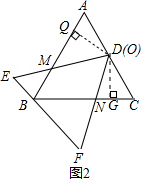
(2)AM•CN的值不会改变.
在△ADM与△CND中,
∵∠A=∠C=60°,∠DNC=∠DBN+∠BDN=30°+α,∠ADM=30°+α,
∴∠ADM=∠CND,
∴△ADM∽△CND
∴$\frac{AD}{CN}=\frac{AM}{CD}$,
∴AM•CN=AD•CD=2×2=4,
∴AM•CN的值不会改变;
(3)情形1,当0°<α<60°时,1<AM<4,即1<x<4,此时两三角形板重叠部分为四边形DMBN,
如图2,过D作DQ⊥AB于Q,DG⊥BC于G,
∴DQ=QG=$\sqrt{3}$,
由(2)知,AM•CN=4,得CN=$\frac{4}{x}$,
于是y=$\frac{\sqrt{3}}{4}$AB2-$\frac{1}{2}$AM•DQ$-\frac{1}{2}CN•DQ$=4$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x$-\frac{2\sqrt{3}}{x}$(1<x<4);
情形2,当60°≤α<90°时,AM≥4时,即x≥4,此时两三角形板重叠部分为△DPN,
如图3,过点D作DH∥BC交AM于H,易证△MBP∽△MHD,
∴$\frac{BP}{DH}$=$\frac{MB}{MH}$,
又∵MB=x-4,MH=x-2,DH=2
∴BP=$\frac{2x-8}{x-2}$,
∴PN=4-$\frac{4}{x}$-$\frac{2x-8}{x-2}$,
于是y=$\frac{1}{2}$PN•DG=$\frac{1}{2}$$•\sqrt{3}$•(4-$\frac{4}{x}$$-\frac{2x-8}{x-2}$)=$\frac{\sqrt{3}x}{x-2}$-$\frac{2\sqrt{3}}{x}$,
综上所述,1<x<4时,y=4$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x$-\frac{2\sqrt{3}}{x}$;x≥4时,y=$\frac{\sqrt{3}x}{x-2}$-$\frac{2\sqrt{3}}{x}$.
点评 本题主要考查了相似三角形的判定和性质、等腰直角三角形的性质以及二次函数等知识的综合应用,分类讨论,综合运用各性质定理是解答此题的关键.

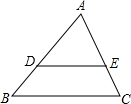 如图,△ABC中,DE∥BC,且AD:DB=2:1,那么DE:BC=2:3.
如图,△ABC中,DE∥BC,且AD:DB=2:1,那么DE:BC=2:3.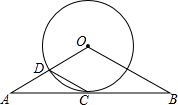 已知:如图,直线AB经过⊙O上的点C,OA与⊙O 交于点D,若OA=OB,AD=CD,∠A=30°
已知:如图,直线AB经过⊙O上的点C,OA与⊙O 交于点D,若OA=OB,AD=CD,∠A=30°