题目内容
13．若关于x的方程$\frac{x+1}{x-2}$=$\frac{m-1}{m-3}$产生增根，则m为3．分析 首先根据分式方程的增根是使分母的值为零的根，求出关于x的方程$\frac{x+1}{x-2}$=$\frac{m-1}{m-3}$的增根是x=2，然后把x=2代入化为整式方程的方程，求出m的值是多少即可．
解答 解：由$\frac{x+1}{x-2}$=$\frac{m-1}{m-3}$，可得
（x-2）（m-1）=（x+1）（m-3），
∵原方程有增根，
∴x-2=0，
∴原方程的增根是x=2，
把x=2代入整式方程，可得
0=（2+1）（m-3）=3（m-3），
解得m=3．
故答案为：3．
点评 此题主要考查了分式方程的增根，要熟练掌握，解答此题的关键是要明确：增根产生的原因、检验增根的方法．
练习册系列答案
相关题目
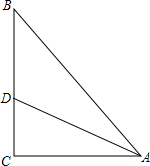在Rt△ABC中，∠C=90°，tan∠CAD=$\frac{\sqrt{3}}{3}$，AB=14，AD=10，求BD的长．