题目内容
11.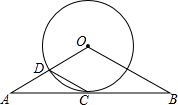 已知:如图,直线AB经过⊙O上的点C,OA与⊙O 交于点D,若OA=OB,AD=CD,∠A=30°
已知:如图,直线AB经过⊙O上的点C,OA与⊙O 交于点D,若OA=OB,AD=CD,∠A=30°(1)求证:直线AB是⊙O的切线;
(2)若AB=4$\sqrt{3}$,求OA的长.
分析 (1)利用已知结合等腰三角形的性质得出∠A以及∠AOC的度数,进而得出∠OCA的度数求出即可;
(2)利用已知得出BC以及AC的值进而求出AC的长.
解答 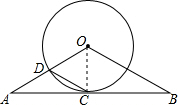 (1)证明:连接OC.
(1)证明:连接OC.
∵AD=CD,∠A=30°,
∴∠A=∠ACD=30°,
∴∠ODC=∠A+∠ACD=60°,
∵OC=OD,
∴∠OCD=∠ODC=60°,
∴∠OCA=∠OCD+∠ACD=90°,
∴直线AB为⊙O的切线;
(2)解:∵OA=OB,OC⊥AB,AB=4$\sqrt{3}$,
∴BC=AC=2$\sqrt{3}$,
∵∠A=30°,
∴OA=2OC,
∵在Rt△ACO中,OA2=OC2+AC2,
∴AC=4.
点评 此题主要考查了切线的判定和勾股定理以及等腰三角形的性质,得出∠AOC的度数是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6.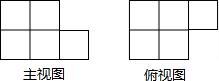 如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )
如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )
 如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )
如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |
16.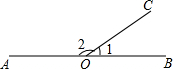 如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
 如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )| A. | $\frac{1}{2}$∠2-∠1 | B. | $\frac{1}{2}$(∠2-∠1) | C. | $\frac{1}{2}$∠2-$\frac{3}{2}$∠1 | D. | $\frac{1}{3}$(∠2+∠1) |
3.下列语句不正确的是( )
| A. | 所有的正比例函数肯定是一次函数 | |
| B. | 一次函数的一般形式是y=kx+b | |
| C. | 正比例函数和一次函数的图象都是直线 | |
| D. | 正比例函数的图象是一条过原点的直线 |
20.不等式组$\left\{\begin{array}{l}{5+2x≥3}\\{\frac{x+1}{3}>\frac{x}{2}}\end{array}\right.$,写出不等式组的整数解是( )
| A. | -1,0,1 | B. | 0,1,2 | C. | -2,-1,0 | D. | 1,2,3 |
1.在代数式$\frac{2}{x+1}$中,x的取值范围是( )
| A. | x>0 | B. | x≤0 | C. | x≠-1 | D. | x≠0 |