题目内容
7.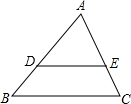 如图,△ABC中,DE∥BC,且AD:DB=2:1,那么DE:BC=2:3.
如图,△ABC中,DE∥BC,且AD:DB=2:1,那么DE:BC=2:3.
分析 先根据相似三角形的判定方法可判断△ADE∽△ABC,则根据相似三角形的性质得$\frac{DE}{BC}$=$\frac{AD}{AB}$,再根据比例的性质由AD:DB=2:1得到$\frac{AD}{AB}$=$\frac{2}{3}$,则即可得到DE与BC的比值.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$,
∵AD:DB=2:1,
∴$\frac{AD}{AB}$=$\frac{2}{2+1}$=$\frac{2}{3}$
∴DE:BC=2:3.
故答案为2:3.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;利用相似比计算相应线段的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.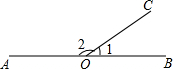 如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
 如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )| A. | $\frac{1}{2}$∠2-∠1 | B. | $\frac{1}{2}$(∠2-∠1) | C. | $\frac{1}{2}$∠2-$\frac{3}{2}$∠1 | D. | $\frac{1}{3}$(∠2+∠1) |
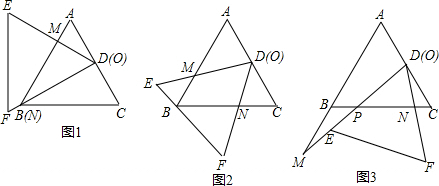
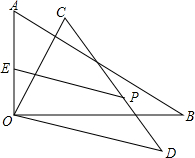 如图在△ABO中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为x(0°<x<180°)得到△COD.设AO中点为E,CD中点为P,AO=6,连接EP,当旋转角x=120°时,EP长度最大,最大值为9.
如图在△ABO中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为x(0°<x<180°)得到△COD.设AO中点为E,CD中点为P,AO=6,连接EP,当旋转角x=120°时,EP长度最大,最大值为9.