题目内容
10. 如图,要使宽为2米的矩形平板车ABCD通过宽为2$\sqrt{2}$米的等宽的直角通道,则平板车的长最多为( )
如图,要使宽为2米的矩形平板车ABCD通过宽为2$\sqrt{2}$米的等宽的直角通道,则平板车的长最多为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
分析 如图,先设平板手推车的长度为x米,则得出x为最大值时,平板手推车所形成的△CBP为等腰直角三角形.连接PO,与BC交于点N,利用△CBP为等腰直角三角形即可求得平板手推车的长度不能超过多少米.
解答 解:设平板手推车的长度为x米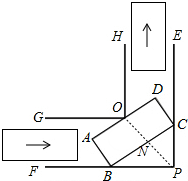 ,
,
当x为最大值,且此时平板手推车所形成的△CBP为等腰直角三角形.
连接PO,与BC交于点N.
∵直角通道的宽为2$\sqrt{2}$m,
∴PO=4m,
∴NP=PO-ON=4-2=2(m).
又∵△CBP为等腰直角三角形,
∴AD=BC=2CN=2NP=4(m).
故选:C.
点评 本题主要考查了勾股定理的应用以及等腰三角形知识,解答的关键是由题意得出要想顺利通过直角通道,此时平板手推车所形成的三角形为等腰直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列运算正确的是( )
| A. | 2a2(1-2a)=2a2-2a3 | B. | a2+a2=a4 | C. | (a+b)2=a2+b2+2ab | D. | (2a+1)(2a-1)=2a2-1 |
5.下列各数不是无理数的是( )
| A. | $\sqrt{7}$ | |
| B. | 0.5 | |
| C. | 0.151151115…(两个5之间依次多一个1) | |
| D. | 2π |
15.若a<b,则下列各不等式中一定成立的是( )
| A. | a-1<b-1 | B. | -a<-b | C. | $\frac{a}{3}>\frac{b}{3}$ | D. | ac<bc |
 在平面直角坐标系xOy中,直线y=kx+b的图象经过(1,0),(-2,3)两点,且与y轴交于点A.
在平面直角坐标系xOy中,直线y=kx+b的图象经过(1,0),(-2,3)两点,且与y轴交于点A. 在矩形ABCD中,∠CAB=30°,将△BAC绕点A按逆时针旋转α度至△AEF的位置,α<60°,试用含α的代数式表示∠EFC.
在矩形ABCD中,∠CAB=30°,将△BAC绕点A按逆时针旋转α度至△AEF的位置,α<60°,试用含α的代数式表示∠EFC. 如图,在△ABC中,∠ACB=120°,将它绕着点C旋转30°后得到△DEC,则∠ACE=150°.
如图,在△ABC中,∠ACB=120°,将它绕着点C旋转30°后得到△DEC,则∠ACE=150°.