题目内容
20. 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
| x | … | -5 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{29}{10}$ | -$\frac{5}{2}$ | -$\frac{13}{6}$ | -2 | -$\frac{5}{2}$ | -$\frac{17}{4}$ | $\frac{17}{4}$ | $\frac{5}{2}$ | 2 | m | $\frac{5}{2}$ | $\frac{29}{10}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
分析 (1)由x在分母上,可得出x≠0;
(2)将x=3代入函数解析式求出y值即可;
(3)连点成线,画出函数图象;
(4)观察函数图象,找出函数的一条性质即可.
解答 解:(1)∵x在分母上,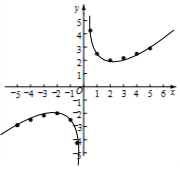
∴x≠0.
故答案为:x≠0.
(2)当x=3时,m=$\frac{3}{2}$+$\frac{2}{3}$=$\frac{13}{6}$.
(3)连点成线,画出函数图象,如图所示.
(4)观察函数图象,可知:当x>2 时,y随x的增大而增大.
故答案为:当x>2 时,y随x的增大而增大.
点评 本题考查了反比例函数的性质、正比例函数的性质、正比例函数的图象以及反比例函数的图象,解题的关键是:(1)由x在分母上找出x≠0;(2)将x=3代入函数解析式求出y值;(3)描点连线,画出函数图象;(4)观察函数图象,找出函数性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.在一年一次的安全知识考试中,其中有10道多项选择题,每题分值相同,每题必答.下面不完整的表格记录了四位同学的得分情况.
(1)分析表格数据,直接填空:答对一道全部选项的题,得5分,答出一道部分选项正确且未选错误项的题,得2分,选出一道有错误选项的题,得-1分;
(2)英英同学有1题答对部分选项且未选错误项,总得分为35分,求英英答对全部选项的题数.
| 学生姓名 | 答对全部选项的题数 | 答对部分选项且未选错误项的题数 | 有错误选项的题数 | 得分 |
| 伍伍 | 10 | 0 | 0 | 50 |
| 佳佳 | 9 | 0 | 1 | 44 |
| 刚刚 | 6 | 2 | 2 | 32 |
| 英英 | 1 | 35 |
(2)英英同学有1题答对部分选项且未选错误项,总得分为35分,求英英答对全部选项的题数.
8.计算(a2)3正确的是( )
| A. | a8 | B. | a6 | C. | a5 | D. | a2 |
9.如果a>b,那么下列不等式的变形中,正确的是( )
| A. | a-1<b-1 | B. | 2a<2b | C. | a-b<0 | D. | -a<-b |
10.要想了解10万名考生的数学成绩,从中抽取了2000名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这2000名考生是总体的一个样本 | B. | 每位考生的数学成绩是个体 | ||
| C. | 10万名考生是个体 | D. | 10万名考生是总体 |
 如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.
如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.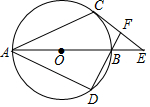 如图,AB为⊙O的直径,AC、AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为2,∠E=45°,则CF的长为4-2$\sqrt{2}$.
如图,AB为⊙O的直径,AC、AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为2,∠E=45°,则CF的长为4-2$\sqrt{2}$.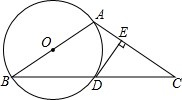 如图,已知△ABC中,AB=AC,以AB为直径的⊙O交 BC于点D,过D作DE⊥AC于E.
如图,已知△ABC中,AB=AC,以AB为直径的⊙O交 BC于点D,过D作DE⊥AC于E.