题目内容
5.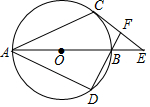 如图,AB为⊙O的直径,AC、AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为2,∠E=45°,则CF的长为4-2$\sqrt{2}$.
如图,AB为⊙O的直径,AC、AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为2,∠E=45°,则CF的长为4-2$\sqrt{2}$.
分析 连接半径OC,由切线性质得:∠OCE=90°,则△OCE是等腰直角三角形,由勾股定理计算OE的长,证明∠EBF=∠EFB,则BE=EF=2$\sqrt{2}$-2,从而得出CF的长.
解答 解:连接OC、BC,
∵$\widehat{BC}$=$\widehat{BD}$,
∴∠BAC=∠DAB,
∵EC是⊙O的切线,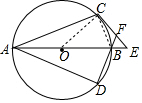
∴∠OCE=90°,
∵∠E=45°,
∴△OCE是等腰直角三角形,
∴OC=CE=2,∠COE=45°,
∵OA=OC,
∴∠BAC=∠ACO=22.5°,
∴∠DAB=22.5°,
即∠DAC=22.5°+22.5°=45°,
∵A、D、B、C四点共圆,
∴∠CBF=∠DAC=45°,
∵∠BCF=∠ACO=22.5°,
∴∠BFE=22.5°+45°=67.5°,
△BFE中,∠FBE=180°-67.5°-45°=67.5°,
∴∠EBF=∠EFB,
∴BE=EF,
Rt△OCE中,OE=2$\sqrt{2}$,
∴BE=AO+OE-AB=2+2$\sqrt{2}$-4=2$\sqrt{2}$-2,
∴EF=BE=2$\sqrt{2}$-2,
∴CF=CE-EF=2-(2$\sqrt{2}$-2)=4-2$\sqrt{2}$,
故答案为:4-2$\sqrt{2}$.
点评 本题考查了切线的性质、四点共圆的性质、等腰直角三角形、等腰三角形的性质和判定、勾股定理,利用角的大小关系得出线段的关系,并根据勾股定理列等式计算边的长,从而使问题得以解决.

练习册系列答案
相关题目
20. 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
| x | … | -5 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{29}{10}$ | -$\frac{5}{2}$ | -$\frac{13}{6}$ | -2 | -$\frac{5}{2}$ | -$\frac{17}{4}$ | $\frac{17}{4}$ | $\frac{5}{2}$ | 2 | m | $\frac{5}{2}$ | $\frac{29}{10}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
 在矩形纸片ABCD中,AD=4cm,AB=10cm,按图所示方式折叠,使点B与点D重合,折痕为EF,求
在矩形纸片ABCD中,AD=4cm,AB=10cm,按图所示方式折叠,使点B与点D重合,折痕为EF,求 如图,在△ABC中,∠ACB=90°,将△ACD沿CD折叠,使点A恰好落在BC边上的点E处.若∠B=25°,则∠BDE=40度.
如图,在△ABC中,∠ACB=90°,将△ACD沿CD折叠,使点A恰好落在BC边上的点E处.若∠B=25°,则∠BDE=40度.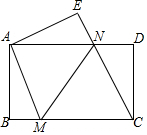 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落住点A处,点D落在点E处,直线MN交BC于点M,交AD于点N
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落住点A处,点D落在点E处,直线MN交BC于点M,交AD于点N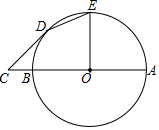 已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2
已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2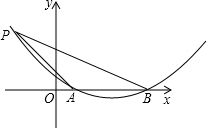 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求:
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求: 如图,长方形硬纸板以其中任意一边为轴旋转都可得到一个圆柱,你认为以3厘米长的边为轴旋转得到的圆柱体积较大.
如图,长方形硬纸板以其中任意一边为轴旋转都可得到一个圆柱,你认为以3厘米长的边为轴旋转得到的圆柱体积较大.