题目内容
10.在一年一次的安全知识考试中,其中有10道多项选择题,每题分值相同,每题必答.下面不完整的表格记录了四位同学的得分情况.| 学生姓名 | 答对全部选项的题数 | 答对部分选项且未选错误项的题数 | 有错误选项的题数 | 得分 |
| 伍伍 | 10 | 0 | 0 | 50 |
| 佳佳 | 9 | 0 | 1 | 44 |
| 刚刚 | 6 | 2 | 2 | 32 |
| 英英 | 1 | 35 |
(2)英英同学有1题答对部分选项且未选错误项,总得分为35分,求英英答对全部选项的题数.
分析 (1)根据表格的得分情况填空;
(2)设英英答对全部选项的题数为x道,则根据(1)中所得的数据和英英同学的得分情况列出方程并解答.
解答 解:(1)由伍伍同学的得分情况知,答对一道全部选项的题得分为:50÷10=5(分).
由佳佳同学的得分情况知,有错误选项的题的题得分为:44-5×9=-1(分).
结合刚刚同学的得分情况知,答出一道部分选项正确且未选错误项的题的得分为:$\frac{1}{2}$(32-6×5+2)=2(分).
故答案是:5;2;-1;
(2)设英英答对全部选项的题数为x道,
依题意得:5x+2-(10-1-x)=35,
则x=7.
答:英英答对全部选项的题数是7道.
点评 本题考查了一元一次方程的应用.根据已知得出等量关系是解题关键.

练习册系列答案
相关题目
5.世界杯期间,有甲、乙两种价格的门票,甲种门票价格为4000元人民币/张,乙种门票价格为3000元人民币/张,牛老师购买这两种价格的门票共6张,花了20000元人民币,求甲、乙两种门票各购买多少张?
2.在下列运算:①m2•m3=m6;②(-2xy)4=8x4y4;③x3n÷xn=x3;④(-5)-2×50=$\frac{1}{5}$;⑤(3.14-π)0=1;⑥2x-2=$\frac{1}{{2{x^2}}}$中,正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.用科学记数法表示数0.000 000 009012正确的是( )
| A. | 0.9012×10-8 | B. | 9.012×10-9 | C. | 9.012×10-10 | D. | 90.12×10-10 |
20. 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
| x | … | -5 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{29}{10}$ | -$\frac{5}{2}$ | -$\frac{13}{6}$ | -2 | -$\frac{5}{2}$ | -$\frac{17}{4}$ | $\frac{17}{4}$ | $\frac{5}{2}$ | 2 | m | $\frac{5}{2}$ | $\frac{29}{10}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
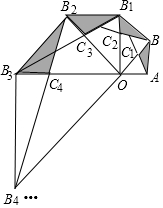 如图,△OAB中,∠OAB=90°,OA=AB=1.以OB为直角边向外作等腰直角三角形OBB1,以OB1为直角边向外作等腰直角三角形OB1B2,以OB2为直角边向外作等腰直角三角形OB2B3,…,连接AB1,BB2,B1B3,…,分别与OB,OB1,OB2,…交于点C1,C2,C3,…,按此规律继续下去,△ABC1的面积记为S1,△BB1C2的面积记为S2,△B1B2C3的面积记为S3,…,则S2017=$\frac{1}{3}$×22015..
如图,△OAB中,∠OAB=90°,OA=AB=1.以OB为直角边向外作等腰直角三角形OBB1,以OB1为直角边向外作等腰直角三角形OB1B2,以OB2为直角边向外作等腰直角三角形OB2B3,…,连接AB1,BB2,B1B3,…,分别与OB,OB1,OB2,…交于点C1,C2,C3,…,按此规律继续下去,△ABC1的面积记为S1,△BB1C2的面积记为S2,△B1B2C3的面积记为S3,…,则S2017=$\frac{1}{3}$×22015..