题目内容
12.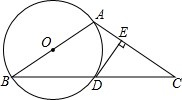 如图,已知△ABC中,AB=AC,以AB为直径的⊙O交 BC于点D,过D作DE⊥AC于E.
如图,已知△ABC中,AB=AC,以AB为直径的⊙O交 BC于点D,过D作DE⊥AC于E.(1)求证:直线DE是⊙O的切线;
(2)若CD=2$\sqrt{3}$,∠ACB=30°,分别求AB,OE的大小.
分析 (1)要想证DE是⊙O的切线,只要连接OD,求证∠ODE=90°即可.
(2)根据三角函数的定义,即可求得AB,再在Rt△CDE中,根据直角三角形的性质,可求得DE,再由勾股定理求出OE即可.
解答 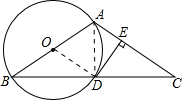 解:(1)连接OD,则OD=OB,
解:(1)连接OD,则OD=OB,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C.
∴OD∥AC,
∴∠ODE=∠DEC=90°,
∴DE是⊙O的切线;
(2)连接AD,
∵AB为直径
∴∠ADB=90°,
∵AB=AC∠ACB=30°
∴BD=DC∠B=∠ACB=30°,
∵CD=2$\sqrt{3}$,
∴BD=2$\sqrt{3}$,
在Rt△ABD中,cos∠B=$\frac{BD}{AB}$,
∴AB=$\frac{BD}{cos∠B}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4,
∴OD=OB=$\frac{1}{2}$AB=2,
在Rt△CDE中,sin∠C=$\frac{DE}{DC}$,
∴DE=DCsin∠C=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$,
在Rt△ODE中,OE2=OD2+DE2=22+($\sqrt{3}$)2=7,
∴OE=$\sqrt{7}$.
点评 本题考查了切线的判定和性质、勾股定理、圆周角定理以及解直角三角形,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
2.在下列运算:①m2•m3=m6;②(-2xy)4=8x4y4;③x3n÷xn=x3;④(-5)-2×50=$\frac{1}{5}$;⑤(3.14-π)0=1;⑥2x-2=$\frac{1}{{2{x^2}}}$中,正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
| x | … | -5 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{29}{10}$ | -$\frac{5}{2}$ | -$\frac{13}{6}$ | -2 | -$\frac{5}{2}$ | -$\frac{17}{4}$ | $\frac{17}{4}$ | $\frac{5}{2}$ | 2 | m | $\frac{5}{2}$ | $\frac{29}{10}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
1.下列分解因式中,结果正确的是( )
| A. | x2-1=(x-1)2 | B. | x2+2x-1=(x+1)2 | C. | x2-6x+9=x(x-6)+9 | D. | 2x2-2=2(x+1)(x-1) |
2.对于不等式2x>-4,下列解集正确的是( )
| A. | x>2 | B. | x>-2 | C. | x<-2 | D. | x>-$\frac{1}{2}$ |
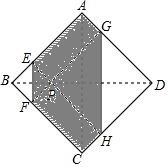 如图,正方形纸片ABCD的边长为2,翻折∠B、∠D.使两个直角的顶点重合于直线BD上一点P.EF与GH为折痕.若BP=$\frac{1}{4}$AC,则图中阴影部分的六边形AEFCHG的面积为$\frac{11}{4}$.
如图,正方形纸片ABCD的边长为2,翻折∠B、∠D.使两个直角的顶点重合于直线BD上一点P.EF与GH为折痕.若BP=$\frac{1}{4}$AC,则图中阴影部分的六边形AEFCHG的面积为$\frac{11}{4}$.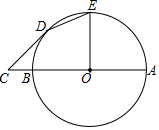 已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2
已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2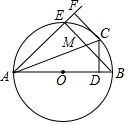 如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.
如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.