题目内容
15. 如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.
如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.
分析 分两种情形①如图1中,当CB=CA′时,易知四边形BCA′M是菱形.②如图2中,当A′B=A′C时,易知MA′∥AC.分别求解即可.
解答 解:分两种情形①如图1中,当CB=CA′时,易知四边形BCA′M是菱形.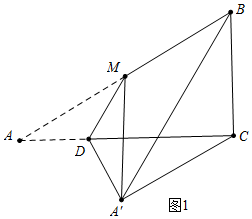
∴∠MA′C=∠ABC=60°,
∵∠MAD=∠MA′D=30°,'
∴∠CA′D=90°,
∵CA′∥AB,
∴∠A′CD=30°,
∴CD=2DA′=2AD,
在Rt△ABC中,∵∠A=30°,BC=6,
∴AC=6$\sqrt{3}$,AB=2BC=12,
∴AD=$\frac{1}{3}$AC=2$\sqrt{3}$.
②如图2中,当A′B=A′C时,易知MA′∥AC.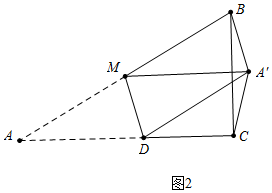
∴∠A′MD=∠ADM=∠AMD,
∴AM=AD,
∵AM=BM,AB=12,
∴AD=6.
故答案为2$\sqrt{3}$或6.
点评 本题考查翻折变换、等腰三角形的性质、直角三角形30度角的性质等知识,解题的关键是西合营4分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.世界杯期间,有甲、乙两种价格的门票,甲种门票价格为4000元人民币/张,乙种门票价格为3000元人民币/张,牛老师购买这两种价格的门票共6张,花了20000元人民币,求甲、乙两种门票各购买多少张?
6.下列各组数能作为直角三角形的三边长的是( )
| A. | 5、6、7 | B. | 4、8、10 | C. | 6、8、10 | D. | 9、15、17 |
20. 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.小奥根据学习函数的经验,对函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质进行了探究.
下面是小奥的探究过程,请补充完整:
(1)函数y=$\frac{x}{2}$+$\frac{2}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值:
| x | … | -5 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{29}{10}$ | -$\frac{5}{2}$ | -$\frac{13}{6}$ | -2 | -$\frac{5}{2}$ | -$\frac{17}{4}$ | $\frac{17}{4}$ | $\frac{5}{2}$ | 2 | m | $\frac{5}{2}$ | $\frac{29}{10}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可):当x>2时,y随x的增大而增大.
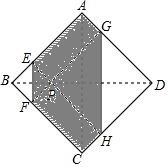 如图,正方形纸片ABCD的边长为2,翻折∠B、∠D.使两个直角的顶点重合于直线BD上一点P.EF与GH为折痕.若BP=$\frac{1}{4}$AC,则图中阴影部分的六边形AEFCHG的面积为$\frac{11}{4}$.
如图,正方形纸片ABCD的边长为2,翻折∠B、∠D.使两个直角的顶点重合于直线BD上一点P.EF与GH为折痕.若BP=$\frac{1}{4}$AC,则图中阴影部分的六边形AEFCHG的面积为$\frac{11}{4}$.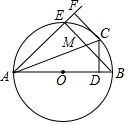 如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.
如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.