题目内容
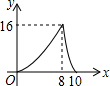
18.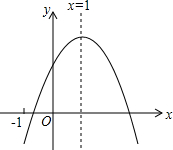 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2-4ac>0,其中正确的结论有②⑤.(只填序号)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2-4ac>0,其中正确的结论有②⑤.(只填序号)
分析 ①:首先根据抛物线开口向下,可得a<0,然后根据对称轴在y轴的右边,可得b>0,最后根据抛物线与y轴的交点在x轴的上方,可得c>0,所以abc<0.
②:根据二次函数y=ax2+bx+c(a≠0)的图象,可得当x=1时,y=a+b+c>0.
③:根据二次函数y=ax2+bx+c(a≠0)的图象,可得当x=2时,y=4a+2b+c>0,据此判断即可.
④:根据二次函数y=ax2+bx+c(a≠0)的图象,可得当x=-1时,y=a-b+c<0,所以b>a+c,据此判断即可.
⑤:根据二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,可得△>0,所以b2-4ac>0,据此判断即可.
解答 解:∵抛物线开口向下,
∴a<0,
∵-$\frac{b}{2a}$>0,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,
∴结论①不正确;
∵当x=1时,y=a+b+c>0,
∴结论②正确;
∵抛物线的对称轴是x=1,抛物线与x轴的一个交点满足:-1<x1<0,
∴抛物线与x轴的另一个交点满足:2<x2<3,
∴当x=2时,y=4a+2b+c>0,
∴结论③不正确;
∵当x=-1时,y=a-b+c<0,
∴b>a+c,
∴结论④不正确;
二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,
∴△>0,
∴b2-4ac>0,
∴结论⑤正确.
∴正确的结论有2个:②⑤.
故答案为:②⑤.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

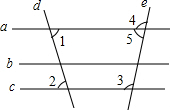 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A. | 若a∥b,b∥c,则a∥c | B. | 若∠1=∠2,则a∥c | ||
| C. | 若∠3=∠2,则b∥c | D. | 若∠3+∠5=180°,则a∥c |
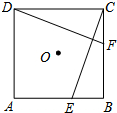 如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为90°.
如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为90°.