题目内容
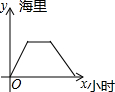
15.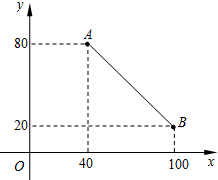 如图,线段AB表示一种产品的销售量y(吨)与销售价格x(元/吨)之间的对应关系.
如图,线段AB表示一种产品的销售量y(吨)与销售价格x(元/吨)之间的对应关系.(1)求y关于x的函数解析式,并写出定义域;
(2)如果销售额为3500元时,问销售量是多少?
分析 (1)设y与x的函数关系式为y=kx+b(k≠0),然后将点A、B的坐标代入得到关于k、b的方程组,从而可解得k、b的值;
(2)销售额=销售量×销售的价格,从而得到关于x的一元二次方程,然后解这个关于x的方程即可求得问题的答案.
解答 解:(1)设y与x的函数关系式为y=kx+b(k≠0),
将A(40,80)、B(100,20)代入得:$\left\{\begin{array}{l}{40k+b=80}\\{100k+b=20}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=120}\end{array}\right.$.
所以y与x的函数关系式为y=-x+120(40≤x≤100);
(2)由销售额=销售量×销售的价格得:x(-x+120)=3500,
解得:x1=50,x2=70,
当x=50时,y=-50+120=70吨;
当x=70时,y=-70+120=50吨.
答:如果销售额为3500元时,问销售量是70吨或50吨.
点评 本题主要考查的是利用待定系数法求一次函数的解析式,以及一元二次方程的应用,读懂题意根据销售额=销售量×销售的价格列出方程是解题的关键.

练习册系列答案
相关题目
10.为筹备班级的初中毕业联欢会,班长对全班同学爱吃哪几种水果作民意调查,从而最终决定买什么水果.下列调查数据中最值得关注的是( )
| A. | 平均数 | B. | 中位数 | C. | 方差 | D. | 众数 |
20.某中学随机调查了15名学生,了解他们一周在学校参加体育锻炼时间,列表如下:
则这15名同学一周在校参加体育锻炼时间的中位数和众数分别是6;6.
| 锻炼时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 2 | 6 | 5 | 2 |
7.直线y=$\frac{1}{2}$x+3与x轴的交点坐标为( )
| A. | (-6,0) | B. | (0,3) | C. | (0,-6) | D. | (3,0) |
4.如图1,将一个边长为a的正方形纸片剪去两个矩形,得到一个“S”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
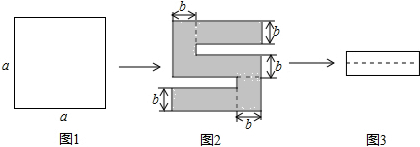

| A. | 2a-3b | B. | 2a-4b | C. | 4a-8b | D. | 4a-10b |
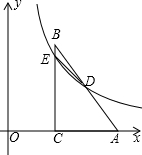 如图,在平面直角坐标系中,Rt△ABC,∠ACB=90°,BC=4,点C的坐标为(2,0),点A坐标为(5,0),点D是AB边上的中点,反比例函数y=$\frac{k}{x}$经过点D,且交BC边于点E.
如图,在平面直角坐标系中,Rt△ABC,∠ACB=90°,BC=4,点C的坐标为(2,0),点A坐标为(5,0),点D是AB边上的中点,反比例函数y=$\frac{k}{x}$经过点D,且交BC边于点E.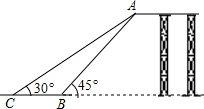 如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.
如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.