题目内容
7．直线y=$\frac{1}{2}$x+3与x轴的交点坐标为（ ）| A． | （-6，0） | B． | （0，3） | C． | （0，-6） | D． | （3，0） |
分析 令y=0求出x的值即可得出直线与x轴的交点坐标．
解答 解：∵令y=0，则x=-6，
∴直线y=$\frac{1}{2}$x+3与x轴的交点坐标为（-6，0），
故选A．
点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
相关题目
18．某次活动课上，要在某个小组中随机挑选2名同学上台表演，已知这个小组共有2名男同学，2名女同学，那么恰好挑选1名男同学和1名女同学的概率是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
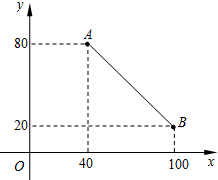如图，线段AB表示一种产品的销售量y（吨）与销售价格x（元/吨）之间的对应关系．
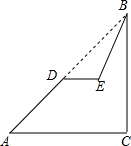如图，已知斜坡AB长为60$\sqrt{2}$米，坡角（即∠BAC）为45°，BC⊥AC．现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE，若修建的斜坡BE的坡比为$\sqrt{3}$：1，求休闲平台DE的长是多少米？（结果保留根号）．
12．|-4|的值是（ ）
| A． | 4 | B． | -4 | C． | 2 | D． | -2 |
16．估计$\sqrt{8}$-2的值在（ ）
| A． | 0到1之间 | B． | 1到2之间 | C． | 2到3之间 | D． | 3至4之间 |
17．已知四边形ABCD的四个顶点的坐标分别为A（-1，0），B（5，0），C（6，2），D（0，2），直线y=kx+2将该四边形分成面积相等的两部分，则k的值为（ ）
| A． | -$\frac{2}{5}$ | B． | -$\frac{2}{9}$ | C． | -$\frac{4}{7}$ | D． | -$\frac{2}{7}$ |