题目内容
5.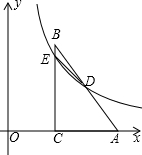 如图,在平面直角坐标系中,Rt△ABC,∠ACB=90°,BC=4,点C的坐标为(2,0),点A坐标为(5,0),点D是AB边上的中点,反比例函数y=$\frac{k}{x}$经过点D,且交BC边于点E.
如图,在平面直角坐标系中,Rt△ABC,∠ACB=90°,BC=4,点C的坐标为(2,0),点A坐标为(5,0),点D是AB边上的中点,反比例函数y=$\frac{k}{x}$经过点D,且交BC边于点E.(1)求反比例函数的解析式;
(2)求△BDE的面积.
分析 (1)先确定B点坐标,再根据线段中点坐标公式得到D($\frac{7}{2}$,2),然后把D点坐标代入y=$\frac{k}{x}$求出k的值即可得到反比例函数解析式;
(2)先根据反比例函数图象上点的坐标特征求出E点坐标,然后根据三角形面积公式求解.
解答 解:(1)∵∠ACB=90°,BC=4,点C的坐标为(2,0),
∴B(2,4),
∵点D是AB边上的中点,点A坐标为(5,0),
∴D($\frac{7}{2}$,2),
把D($\frac{7}{2}$,2)代入y=$\frac{k}{x}$得k=$\frac{7}{2}$×2=7,
∴反比例函数解析式为y=$\frac{7}{x}$;
(2)当x=2时,y=$\frac{7}{x}$=$\frac{7}{2}$,则E(2,$\frac{7}{2}$),
∴S△BDE=$\frac{1}{2}$×(4-$\frac{7}{2}$)×($\frac{7}{2}$-2)=$\frac{3}{8}$.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了反比例函数图象上点的坐标特征和三角形面积公式.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
16.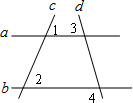 如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
 如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )| A. | 35° | B. | 70° | C. | 90° | D. | 110° |
13.若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m,n(m<n),方程x2+ax+b=2有两个不同的实数根p,q(p<q),则m,n,p,q的大小关系为( )
| A. | p<m<n<q | B. | m<p<q<n | C. | m<p<n<q | D. | p<m<q<n |
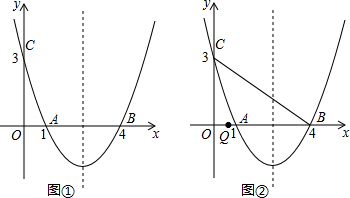
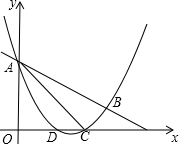 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),C(3,0).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),C(3,0).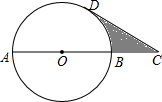 如图,AB为⊙O的直径,点C在AB的延长线上,且AB=2BC=4,CD与⊙O相切于点D,则图中阴影部分的面积是2$\sqrt{3}$-$\frac{2}{3}$π.(结果保留根号和π)
如图,AB为⊙O的直径,点C在AB的延长线上,且AB=2BC=4,CD与⊙O相切于点D,则图中阴影部分的面积是2$\sqrt{3}$-$\frac{2}{3}$π.(结果保留根号和π)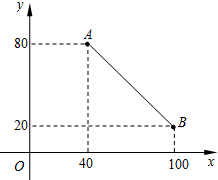 如图,线段AB表示一种产品的销售量y(吨)与销售价格x(元/吨)之间的对应关系.
如图,线段AB表示一种产品的销售量y(吨)与销售价格x(元/吨)之间的对应关系.