题目内容
3.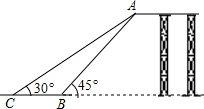 如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.
如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.
分析 根据AB长为4米,∠ABD=45°,求出AD、BD的长度,然后根据∠ACD=30°求出AC、CD的长度,由BC=CD-BD求出BC.
解答 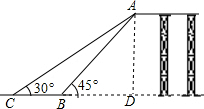 解:过A作AD⊥BC于D,
解:过A作AD⊥BC于D,
在Rt△ABD中,AB=4,∠ABD=45°,
∵sin∠ABD=$\frac{AD}{AB}$,
∴AD=AB•sin45°=$4×\frac{\sqrt{2}}{2}$=2$\sqrt{2}$(米),
∴BD=AD=2$\sqrt{2}$(米),
在Rt△ACD中,∠ACD=30°
∵sin$∠ACD=\frac{AD}{AC}$,
∴AC=$\frac{AD}{sin30°}$=$\frac{2\sqrt{2}}{\frac{1}{2}}$=4$\sqrt{2}$(米),
∴CD=$\sqrt{{AC}^{2}{-AD}^{2}}$=$\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{6}$(米),
∴BC=CD-BD=2$\sqrt{6}$-2$\sqrt{2}$=2($\sqrt{6}$-$\sqrt{2}$)(米).
答:改造后滑梯AC的长为4$\sqrt{2}$米,新、旧滑梯着地点C、B之间的距离为2($\sqrt{6}$-$\sqrt{2}$)米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
相关题目
13.若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m,n(m<n),方程x2+ax+b=2有两个不同的实数根p,q(p<q),则m,n,p,q的大小关系为( )
| A. | p<m<n<q | B. | m<p<q<n | C. | m<p<n<q | D. | p<m<q<n |
18.某次活动课上,要在某个小组中随机挑选2名同学上台表演,已知这个小组共有2名男同学,2名女同学,那么恰好挑选1名男同学和1名女同学的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
12.|-4|的值是( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
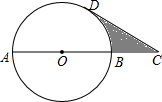 如图,AB为⊙O的直径,点C在AB的延长线上,且AB=2BC=4,CD与⊙O相切于点D,则图中阴影部分的面积是2$\sqrt{3}$-$\frac{2}{3}$π.(结果保留根号和π)
如图,AB为⊙O的直径,点C在AB的延长线上,且AB=2BC=4,CD与⊙O相切于点D,则图中阴影部分的面积是2$\sqrt{3}$-$\frac{2}{3}$π.(结果保留根号和π)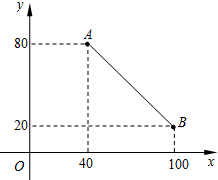 如图,线段AB表示一种产品的销售量y(吨)与销售价格x(元/吨)之间的对应关系.
如图,线段AB表示一种产品的销售量y(吨)与销售价格x(元/吨)之间的对应关系.