题目内容
14．
如图，将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上，如果∠1=25°，那么∠2的度数是（ ）| A． | 53° | B． | 55° | C． | 57° | D． | 60° |
分析 根据三角形的一个外角等于与它不相邻的两个内角的和求出∠3，再根据两直线平行，同位角相等可得∠2=∠3．
解答 解：由三角形的外角性质，
∠3=30°+∠1=30°+25°=55°，
∵矩形的对边平行，
∴∠2=∠3=55°．
故选：B．
点评 本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t（s）．
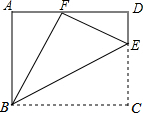如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上．若sin∠DFE=$\frac{1}{3}$，则 tan∠EBC的值为$\frac{\sqrt{2}}{2}$．
9．若过点P和点A（3，2）的直线平行于x轴，过点P和B（-1，-2）的直线平行于y轴，则点P的坐标为（ ）
| A． | （-1，2 ） | B． | （-2，2） | C． | （3，-1） | D． | （3，-2） |
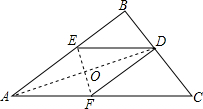如图，在三角形纸片ABC中，∠BAC为锐角，AB=12cm，AC=15cm．按下列步骤折叠：第一次，把∠B折叠使点B落在AC边上，折痕为AD，交BC于点D；第二次折叠，使点A与点D重合，折痕分别交AB、AC于点E、F，EF与AD交于点O，展开后，连结DE、DF．
3．
如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（ ）
如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（ ）| A． | 70° | B． | 50° | C． | 40° | D． | 80° |
4．下列运算正确的是（ ）
| A． | （-2ab）•（-3ab）3=-54a4b4 | B． | （3.5×105）÷（5×106）=7 | ||
| C． | （-0.16）•（-10b2）3=-b7 | D． | （2×10n）（$\frac{1}{2}$×10n）=102n |