题目内容
8. 如图,直径为AB的⊙O交Rt△BCD的两条直角边BC、CD于点E、F,且$\widehat{AF}$=$\widehat{EF}$,连接BF.
如图,直径为AB的⊙O交Rt△BCD的两条直角边BC、CD于点E、F,且$\widehat{AF}$=$\widehat{EF}$,连接BF.(1)求证:CD为⊙O的切线;
(2)当CF=1且∠D=30°时,求AD长.
分析 (1)连接OF,只要证明OF∥BC,即可推出OF⊥CD,由此即可解决问题.
(2)连接AF.思想在Rt△BCF中,求出BC,再在Rt△DBC中,求出DB,在Rt△ABF中,求出AB,根据AD=DB-AB即可解决问题.
解答 (1)证明:连接OF.
∵$\widehat{AF}=\widehat{EF}$,
∴∠CBF=∠FBA,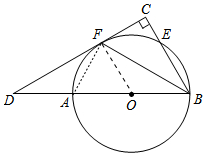
∵OF=OB,
∴∠FBO=∠OFB,
∴∠CBF=∠OFB,
∴BC∥OF,
∴∠OFC+∠C=180°,
∵∠C=90°,
∴∠OFC=90°,即OF⊥DC,
∴CD为⊙O的切线.
(2)解:连接AF.
∵∠D=30°,∠C=90°,
∴∠CBD=60°
∵$\widehat{AF}=\widehat{EF}$,
∴∠CBF=∠DBF=$\frac{1}{2}$∠CBD=30°,
在Rt△BCF中,∵FC=1,∠CBF=30°,
∴BF=2CF=2.
∴BC=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵AB是⊙O的直径,
∴∠AFB=90°,
在Rt△AFB中,∵∠ABF=30°,BF=2,
∴AF=$\frac{1}{2}$AB.
∴AB2=($\frac{1}{2}$AB)2+BF2,即$\frac{3}{4}$AB2=4,AB=$\frac{4\sqrt{3}}{3}$,
在Rt△DCB中,∵∠D=30°,BC=$\sqrt{3}$,
∴BD=2BC=2$\sqrt{3}$.
∴AD=DB-AB=2$\sqrt{3}$-$\frac{{4\sqrt{3}}}{3}$=$\frac{{2\sqrt{3}}}{3}$.
点评 本题考查切线的判定、直角三角形30度角的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案| A. | 由a=b,得$\frac{a}{-4}$=$\frac{b}{-4}$ | B. | 由-3x=-3y,得x=-y | ||
| C. | 由$\frac{x}{4}$=1,得x=$\frac{1}{4}$ | D. | 由x=y,得$\frac{x}{a}$=$\frac{y}{a}$ |
| A. | $\frac{1000}{x}$=$\frac{800}{x-20}$ | B. | $\frac{1000}{x}$=$\frac{800}{x+20}$ | C. | $\frac{1000}{x-20}$=$\frac{800}{x}$ | D. | $\frac{1000}{x+20}$=$\frac{800}{x}$ |
| A. | 6 | B. | 6 $\sqrt{3}$ | C. | 12 $\sqrt{3}$ | D. | 18 |
 如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.