题目内容
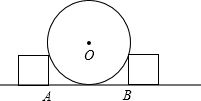 在汽车车轮修理厂,工人师傅常常用两个棱长相等的正方体卡住车轮.如图是其截面图(正方体棱长小于车轮半径).
在汽车车轮修理厂,工人师傅常常用两个棱长相等的正方体卡住车轮.如图是其截面图(正方体棱长小于车轮半径).(1)若正方体之间的距离AB=80cm,正方体棱长为20cm,求车轮半径;
(2)设正方体棱长为a,AB=2b,请你推导求直径d的公式.
考点:垂径定理的应用,勾股定理
专题:
分析:(1)设切点为P,如图,小正方形的顶点分别为C,D,连接CD,OD,OP,OP与CD交于点E,由圆O与AB相切于P,根据切线的性质得到OP与AB垂直,又CD与AB平行,故OP与CD也垂直,根据垂径定理得到E为CD中点,构成直角三角形ODE,设出半径为r,根据DE=AP=40cm,EP=AD=20,分别表示出DE和OE,在直角三角形ODE中,根据勾股定理列出关于r的方程,求出方程的解即可得到半径r的值,
(2)设切点为P,如图,小正方形的顶点分别为C,D,连接CD,OD,OP,OP与CD交于点E,由圆O与AB相切于P,根据切线的性质得到OP与AB垂直,又因为CD与AB平行,故OP与CD也垂直,根据垂径定理得到E为CD中点,构成直角三角形ODE,设出半径为r,根据DE=AP=b,EP=AD=a,分别表示出DE和OE,在直角三角形ODE中,根据勾股定理列出关于r的方程,求出方程的解即可得到半径r的值,进而求出直径d的值.
(2)设切点为P,如图,小正方形的顶点分别为C,D,连接CD,OD,OP,OP与CD交于点E,由圆O与AB相切于P,根据切线的性质得到OP与AB垂直,又因为CD与AB平行,故OP与CD也垂直,根据垂径定理得到E为CD中点,构成直角三角形ODE,设出半径为r,根据DE=AP=b,EP=AD=a,分别表示出DE和OE,在直角三角形ODE中,根据勾股定理列出关于r的方程,求出方程的解即可得到半径r的值,进而求出直径d的值.
解答: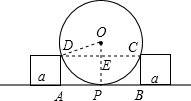 解:(1)如图,设切点为P,小正方形在圆上的顶点分别为C,D,
解:(1)如图,设切点为P,小正方形在圆上的顶点分别为C,D,
连接CD,OD,OP,OP与CD交于E,则OP⊥AB,
故OP⊥CD,E为CD中点,设半径为r,
在Rt△ODE中,DE=40cm,OD=r,OE=r-20,
∴根据勾股定理得:(r-20)2+402=r2,
解得r=50cm.
(2)如图,设切点为P,小正方形在圆上的顶点分别为C,D,
连接CD,OD,OP,OP与CD交于E,则OP⊥AB,
故OP⊥CD,E为CD中点,设半径为r,
在Rt△ODE中,DE=b,OD=r,OE=r-a,
∴根据勾股定理得:(r-a)2+b2=r2,
∴r=
,
则d=2r=
.
 解:(1)如图,设切点为P,小正方形在圆上的顶点分别为C,D,
解:(1)如图,设切点为P,小正方形在圆上的顶点分别为C,D,连接CD,OD,OP,OP与CD交于E,则OP⊥AB,
故OP⊥CD,E为CD中点,设半径为r,
在Rt△ODE中,DE=40cm,OD=r,OE=r-20,
∴根据勾股定理得:(r-20)2+402=r2,
解得r=50cm.
(2)如图,设切点为P,小正方形在圆上的顶点分别为C,D,
连接CD,OD,OP,OP与CD交于E,则OP⊥AB,
故OP⊥CD,E为CD中点,设半径为r,
在Rt△ODE中,DE=b,OD=r,OE=r-a,
∴根据勾股定理得:(r-a)2+b2=r2,
∴r=
| a2+b2 |
| 2a |
则d=2r=
| a2+b2 |
| a |
点评:此题考查了切线的性质,垂径定理,以及勾股定理,本题的关键是根据题意作出辅助线,构造直角三角形,利用数形结合思想及方程的思想来解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列实数中,无理数的是( )
A、
| ||
| B、π | ||
C、
| ||
| D、|-2| |
已知二次函数y=x2-2x+3+k的图象上有三点A(
,y1)、B(3,y2)、C(-
,y3),则y1、y2、y3的大小关系是( )
| 3 |
| 2 |
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y3>y1>y2 |
| D、y3>y2>y1 |
 如图所示,在长和宽分别是a,b的长方形形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a,b的长方形形纸片的四个角都剪去一个边长为x的正方形. 如图,△ABC中,DE∥BC,且AD:DB=2:3,则S△ADE:S△梯形DBCE=
如图,△ABC中,DE∥BC,且AD:DB=2:3,则S△ADE:S△梯形DBCE=