题目内容
已知二次函数y=x2-2x+3+k的图象上有三点A(
,y1)、B(3,y2)、C(-
,y3),则y1、y2、y3的大小关系是( )
| 3 |
| 2 |
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y3>y1>y2 |
| D、y3>y2>y1 |
考点:二次函数图象上点的坐标特征
专题:计算题
分析:根据二次函数图象上点的坐标特征,分别计算出自变量为
、3、-
所对应的函数值,然后比较函数值的大小即可.
| 3 |
| 2 |
解答:解:∵二次函数y=x2-2x+3+k的图象上有三点A(
,y1)、B(3,y2)、C(-
,y3),
∴y1=x2-2x+3+k=3-2
+3+k=6-
+k,y2=x2-2x+3+k=9-6+3+k=6+k,y3=x2-2x+3+k=2+2
+3+k=5+2
+k,
∴y1<y2<y3.
故选D.
| 3 |
| 2 |
∴y1=x2-2x+3+k=3-2
| 3 |
| 3 |
| 2 |
| 2 |
∴y1<y2<y3.
故选D.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了实数的运算和大小比较.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
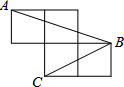 如图,每个小正方形的边长为1,则∠ABC的度数为( )
如图,每个小正方形的边长为1,则∠ABC的度数为( )| A、90° | B、60° |
| C、45° | D、30° |
两个有理数相乘,积是负数,则这两个有理数( )
| A、都是负数 | B、都是正数 |
| C、一正数一负数 | D、有一个是零 |
下列方程中,是一元二次方程的是( )
| A、x2+y2=1 | ||||
B、
| ||||
| C、4x2-5x-3=5 | ||||
D、
|
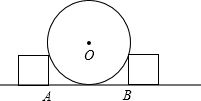 在汽车车轮修理厂,工人师傅常常用两个棱长相等的正方体卡住车轮.如图是其截面图(正方体棱长小于车轮半径).
在汽车车轮修理厂,工人师傅常常用两个棱长相等的正方体卡住车轮.如图是其截面图(正方体棱长小于车轮半径).