题目内容
如图，△ABC中，DE∥BC，且AD：DB=2：3，则S△ADE：S△梯形DBCE=考点：相似三角形的判定与性质
专题：
分析：证明△ADE∽△ABC，进而证明
=(
)2=
，即可解决问题．
| S△ADE |
| S△ABC |
| AD |
| AB |
| 4 |
| 25 |
解答：解：∵DE∥BC，且AD：DB=2：3，
∴△ADE∽△ABC，
=(
)2=
，
∴
=
，
故答案为4：21．
解：∵DE∥BC，且AD：DB=2：3，∴△ADE∽△ABC，
| S△ADE |
| S△ABC |
| AD |
| AB |
| 4 |
| 25 |
∴
| S△ADE |
| S梯形DBCE |
| 4 |
| 21 |
故答案为4：21．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；应牢固掌握相似三角形的判定及其性质，并能灵活运用、解题．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
在直角三角形ABC中，∠C=90°，a=6，b=8，则c=（ ）
| A、7 | B、8 | C、9 | D、10 |
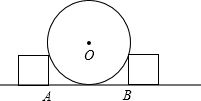在汽车车轮修理厂，工人师傅常常用两个棱长相等的正方体卡住车轮．如图是其截面图（正方体棱长小于车轮半径）．