题目内容
16.已知动点P以每秒2cm的速度沿如图甲所示的边框按B→C→D→E→F→A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙所示,若AB=6cm,试回答下列问题:(1)如图甲,BC的长是多少?如图乙,图中的a是多少?b是多少?
(2)求出点P在F→A上运动时S与t的函数关系式.
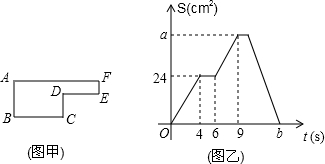
分析 (1)根据动点P以每秒2cm的速度,从B到C用的时间为4s,可以求得BC的长度;根据三角形的面积等于底乘以高除以2,可以得到a的值;根据题意和图形可以得到BC、CD、DE、EF、FA的长,从而可以得到b的值;
(2)设出点P在F→A上运动时S与t的函数关系式为y=kx+b,把(10,24),(17.0)代入y=kx+b即可得到结论.
解答 解:(1)由图象可得,
点P从点B到点C运动的时间是4s,运动的速度是每秒2cm,
故BC的长度是:4×2=8cm,
即BC长是8cm;
∵BC=8cm,AB=6cm,
∴S=$\frac{BC•AB}{2}$=$\frac{8×6}{2}$=24,
即图乙中a的值为24cm2;
由题意可得,
b=$\frac{BC+CD+DE+EF+FA}{2}$=$\frac{8+4+6+(6-4)+(6+8)}{2}$=17s,
即b的值是17s;
(2)设出点P在F→A上运动时S与t的函数关系式为y=kx+b,
把(10,24),(17.0)代入y=kx+b得$\left\{\begin{array}{l}{24=10k+b}\\{0=17k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{24}{7}}\\{b=\frac{408}{7}}\end{array}\right.$,
∴出点P在F→A上运动时S与t的函数关系式为y=-$\frac{24}{7}$x+$\frac{408}{7}$.
点评 本题主要考查了动点问题的函数图象,解决问题的关键是深刻理解动点的函数图象所代表的实际意义,理解动点的完整运动过程,从函数图象中获取相关的信息进行计算.

练习册系列答案
相关题目
1.x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,则(1+$\frac{1}{y}$)(1-$\frac{1}{x}$)=( )
| A. | $4\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{3}{2}$ |
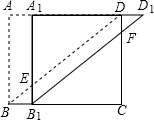 如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1,点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.
如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1,点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F. 如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO.
如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO. 矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).
矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).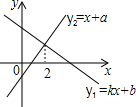 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的序号是①.
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的序号是①.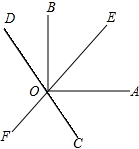 如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC=1:2.
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC=1:2.