题目内容
15. 如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO.
如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO.(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.
分析 (1)连结OC,如图,由PC2=PE•PO和公共角可判断△PCE∽△POC,则∠PEC=∠PCO=90°,然后根据切线的判定定理可判断PC是⊙O的切线;
(2)设OE=x,则EA=2x,OA=OC=3x,证明△OCE∽△OPC,利用相似比可表示出OP,则可列方程3x+6=9x,然后解出x即可得到⊙O的半径.
解答 (1)证明:连结OC,如图,
∵CD⊥AB,
∴∠PEC=90°,
∵PC2=PE•PO,
∴PC:PO=PE:PC,
而∠CPE=∠OPC,
∴△PCE∽△POC,
∴∠PEC=∠PCO=90°,
∴OC⊥PC,
∴PC是⊙O的切线;
(2)解:设OE=x,则EA=2x,OA=OC=3x, ∵∠COE=∠POC,∠OEC=∠OCP,
∵∠COE=∠POC,∠OEC=∠OCP,
∴△OCE∽△OPC,
∴OC:OP=OE:OC,即3x:OP=x:3x,解得OP=9x,
∴3x+6=9x,解得x=1,
∴OC=3,
即⊙O的半径为3.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.也考查了切线的判定方法.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
6.已知点(x1,y1)和(x2,y2)都在函数y=-2x+4的图象上.则下列结论正确的是( )
| A. | 若y1<y2,则x1<x2 | |
| B. | 若y1-y2=2,则x1-x2=-1 | |
| C. | 可由直线y=2x向上平移4个单位得到 | |
| D. | 与坐标系围成的三角形面积为8 |
3.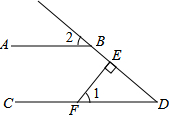 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
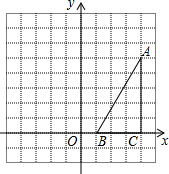 如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:①画出平移后的△A′B′C′.②直接写出点A′、B′、C′的坐标.
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:①画出平移后的△A′B′C′.②直接写出点A′、B′、C′的坐标.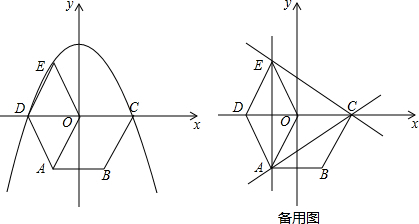
 如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.
如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.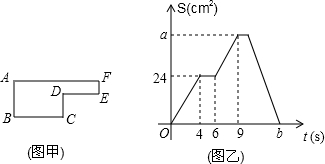
 问题情境:
问题情境: