题目内容
14.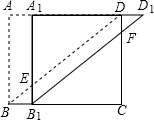 如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1,点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.
如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1,点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.(1)求证:四边形EB1FD是平行四边形;
(2)若AB=3,BC=4,AA1=1,求B1F的长.
分析 (1)欲证明四边形EB1FD是平行四边形,只要证明DE∥B1F,B1E∥DF即可.
(2)由△CB1F∽△CBD,得$\frac{C{B}_{1}}{CB}$=$\frac{{B}_{1}F}{BD}$由此即可解决问题.
解答 (1)证明: ∵△A1B1D1是由△ABD平移所得,
∵△A1B1D1是由△ABD平移所得,
∴AB∥A1B1,BD∥B1D1,
∵四边形ABCD是矩形,
∴AB∥CD,
∴A1B1∥CD,
∴四边形EB1FD是平行四边形.
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,AB=CD=3,AD=BC=4,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=5,
∵AA1=BB1=1,
∴CB1=3,
∵FB1∥BD,
∴△CB1F∽△CBD,
∴$\frac{C{B}_{1}}{CB}$=$\frac{{B}_{1}F}{BD}$,
∴$\frac{3}{4}$=$\frac{{B}_{1}F}{5}$,
∴B1F=$\frac{15}{4}$.
点评 本题考查矩形的性质、平行四边形的性质、平移变换、相似三角形的判定和性质等知识,解题的关键是利用了平移的性质以及相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.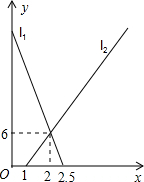 小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
 小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )| A. | 12 km/h,3 km/h | B. | 15km/h,3km/h | C. | 12 km/h,6 km/h | D. | 15km/h,6km/h |
6.已知点(x1,y1)和(x2,y2)都在函数y=-2x+4的图象上.则下列结论正确的是( )
| A. | 若y1<y2,则x1<x2 | |
| B. | 若y1-y2=2,则x1-x2=-1 | |
| C. | 可由直线y=2x向上平移4个单位得到 | |
| D. | 与坐标系围成的三角形面积为8 |
3.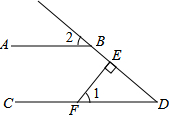 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
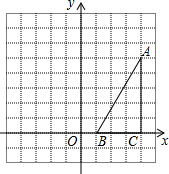 如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:①画出平移后的△A′B′C′.②直接写出点A′、B′、C′的坐标.
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:①画出平移后的△A′B′C′.②直接写出点A′、B′、C′的坐标.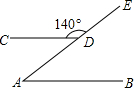 如图,点D在射线AE上,AB∥CD,∠CDE=140°,求∠A的度数.
如图,点D在射线AE上,AB∥CD,∠CDE=140°,求∠A的度数.